Связи и их реакции. Аксиома связей

Всякое твердое тело, которое может занимать произвольное положение в пространстве, называется свободным. Если же на тело наложены условия, ограничивающие свободу его перемещения, тело называется несвободным, а условия, ограничивающие свободу перемещения, – связями. Можно считать, что эффект действия связей такой же, как и действие сил. Силы, с которыми связи действуют на рассматриваемое тело, называются реакциями связей.

Величина и направление реакции связи зависит от действующих сил, поэтому они являются пассивными силами, а задаваемые силы – активными.

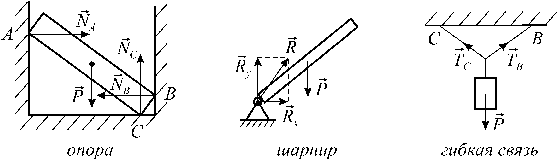
Аксиома связей. Не изменяя кинематического состояния твердого тела, каждую связь, наложенную на тело, можно отбросить, заменив ее действие силой реакции отброшенной связи.

Эта аксиома позволяет рассматривать тело как свободное, но находящееся под действием как активных, так и реактивных сил.

Равновесие сходящейся системы сил

П усть имеется система сил ( ), линии действия которых пересекаются в одной точке. Такая система сил называется сходящейся.

Перенесем все силы вдоль линий их действия в точку О, т.е. заменим её другой системой сил, приложенных в точке О. Равнодействующая такой системы равна векторной сумме данных сил, и линия её действия проходит через точку О. Зная, что все силы можно заменить равнодействующей, можно сформировать условие равновесия твердого тела под действием такой системы сил, а именно: для того чтобы твердое тело, находящееся под действием сходящейся системы сил, было в равновесии, необходимо и достаточно, чтобы равнодействующая этих сил равнялась нулю:

.

Геометрическое условие состоит в том, что силовой многоугольник, построенный на слагаемых силах, должен быть замкнутым, т.к. геометрически равнодействующая изображается вектором, замыкающим силовой многоугольник.

Из равенства следует, что , если или

.

Для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трёх координатных осей равнялась нулю. Данное положение выражает аналитическое условие равновесия сходящейся системы сил.

Если все силы расположены в одной плоскости xOy, то достаточно двух уравнений в системе:

.

Задачи, в которых число неизвестных не превышает числа уравнений равновесия, называются статически определимыми; если число неизвестных превышает число уравнений – статически неопределимыми.

Н апример, для системы, изображенной на рисунке, можно составить только два уравнения равновесия, т.к. система сил плоская, а неизвестных – три (Т_А, Т_С и Т_В). Такая задача является статически неопределимой и решается с учетом деформаций в курсе «Сопротивление материалов».

Теорема о трех силах

Если твердое тело находится в равновесии под действием трёх непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Д оказательство. Перенесем силы и вдоль линий их действия в точку О в соответствии с аксиомой А 2. По аксиоме А 3 сложим эти силы. Т.к. тело находится в равновесии, то из аксиомы А 1 следует, что , и эти силы лежат на одной прямой.