
- •Конспект лекций по теоретической механике
- •Введение
- •Лекция 1 основные понятия статики. Аксиомы статики
- •Основные понятия
- •Аксиомы статики
- •Связи и их реакции. Аксиома связей
- •Равновесие сходящейся системы сил
- •Теорема о трех силах
- •Лекция 2 равновесие плоской системы сил
- •Сложение двух параллельных сил, направленных в одну сторону
- •Сложение двух параллельных сил, направленных в противоположные стороны
- •Пара сил и её свойства
- •Условие равновесия пар
- •Момент силы относительно центра
- •Плоская система сил
- •Приведение произвольной плоской системы сил к данному центру
- •Теорема Вариньона
- •Условия равновесия плоской системы сил
- •Лекция 3 равновесие пространственной системы сил. Центр тяжести
- •Пространственная система сил. Равнодействующая пространственной системы сходящихся сил
- •Равновесие пространственной системы сходящихся сил
- •Момент силы относительно оси
- •Равновесие произвольной пространственной системы сил
- •Частные случаи равновесия
- •Сила тяжести и центр тяжести однородных тел
- •Координаты центров тяжести однородных тел
- •Лекция 4 кинематика точки
- •Аналитические способы задания движения точки в пространстве
- •Векторно-координатный способ задания движения точки
- •Естественный способ задания движения точки
- •Определение скорости точки при различных способах задания движения
- •Векторно-координатный способ задания движения
- •Естественный способ задания движения
- •Определение ускорения точки при различных способах задания движения
- •Векторно-координатный способ задания движения
- •Естественный способ задания движения точки. Понятие о естественном трехграннике
- •Частные случаи движения точки
- •Лекция 5 простейшие движения твердого тела
- •Поступательное движение твердого тела
- •Вращение твердого тела вокруг неподвижной оси
- •Угловая скорость
- •Угловое ускорение
- •Равномерное и равнопеременное вращение
- •Определение скоростей и ускорений точек вращающегося тела. Скорости точек тела
- •Лекция 6 плоскопараллельное движение твердого тела (определение скоростей)
- •Разложение плоского движения твердого тела на поступательное и вращательное
- •Определение скоростей точек твердого тела
- •Теорема о проекциях скоростей двух точек тела
- •Мгновенный центр скоростей
- •Частные случаи определения мгновенного центра скоростей
- •План скоростей
- •Лекция 7 плоскопараллельное движение твердого тела (определение ускорений)
- •Лекция 8 динамика точки
- •Законы классической механики
- •Задачи динамики
- •Дифференциальные уравнения движения точки
- •Дифференциальные уравнения в проекциях на оси естественного трехгранника
- •Алгоритм решения основной задачи динамики
- •Лекция 9 динамика механической системы
- •Теорема о движении центра масс механической системы
- •Закон сохранения движения центра масс
- •Момент инерции тела относительно оси, радиус инерции
- •Моменты инерции некоторых тел
- •1. Тонкий однородный стержень длиной l и массой м.
- •2. Тонкое круглое однородное кольцо радиусом r и массой м.
- •3. Круглая однородная пластина (диск).
- •Момент инерции тела относительно параллельных осей
- •Лекция 10 теорема об изменении количества движения механической системы
- •Закон сохранения количества движения
- •Лекция 11 главный момент количеств движения (кинетический момент) системы относительно центра и оси
- •Закон сохранения момента количества движения точки
- •Кинетический момент вращающегося тела
- •Теорема об изменении главного момента количеств движения механической системы (теорема моментов)
- •Законы сохранения главного момента количеств движения
- •Частный случай вращающейся системы
- •Лекция 12 теорема об изменении кинетической энергии
- •Графический способ вычисления работы
- •Мощность
- •Примеры вычисления работы
- •Кинетическая энергия точки
- •Кинетическая энергия системы
- •Теорема об изменении кинетической энергии системы
- •Система с идеальными связями
- •Вычисление работы сил, приложенных к вращающемуся телу
- •Лекция 13 принцип даламбера
- •Приведение сил инерции твердого тела
- •Динамические реакции, действующие на ось вращающегося тела
- •Лекция 14 принцип возможных перемещений. Принцип даламбера – лагранжа (общее уравнение динамики)
- •Классификация связей
- •Возможные (виртуальные) перемещения
- •Число степеней свободы
- •Идеальные связи
- •Принцип возможных перемещений
- •Равновесие рычага (золотое правило механики)
- •Принцип Даламбера–Лагранжа (общее уравнение динамики)
- •Лекция 15 уравнения лагранжа -го рода
- •Обобщенные силы
- •Примеры вычисления обобщенной силы
- •Условие равновесия системы в обобщенных силах
- •Уравнения Лагранжа
- •Лекция 16 элементарная теория удара твердых тел
- •Основное уравнение теории удара
- •Общие теоремы теории удара
- •Коэффициент восстановления при ударе
- •Экспериментальное определение коэффициента восстановления
- •Прямой центральный удар двух тел (удар шаров)
- •Рекомендуемая литература
- •Содержание
- •Конспект лекций по теоретической механике
Лекция 15 уравнения лагранжа -го рода
Обобщенные координаты системы. Обобщенные силы и способ их вычисления. Уравнения Лагранжа -го рода
Обобщенными координатами механической системы называются величины, заданием которых вполне определяется положение всех точек системы.
Числом степеней свободы системы называется число независимых обобщенных координат, определяющих положение точек системы.

Рассмотрим механическую систему, состоящую из п материальных точек М1, М2, … Мп, имеющую К степеней свободы. Обозначим ее независимые обобщенные координаты q1, q2, … qk. Они вполне определяют положение всех точек системы. Тогда декартовы координаты системы будут функциями обобщенных координат:

Эти соотношения имеют место только в том случае, когда связи не зависят от времени. Возможно существование связей, изменяющихся с течением времени.

Пример: нить маятника тянут за конец А с постоянной скоростью V.
Пусть ОМ = l
, тогда
![]() ,
,
![]()
Очевидно, что в данной задаче декартовы координаты – не только функции обобщенной координаты , но и времени t.
В этом случае имеем:

Связи, не зависящие от времени, называются склерономными (или стационарными), а изменяемые с течением времени – реономными (или нестационарными).
Обобщенные силы

Рассмотрим механическую
систему, состоящую из п материальных
точек: М1,
М2,
… Мп, имеющую К степеней
свободы. Обозначим ее независимые
обобщенные координаты q1,
q2,
… qk.
Предположим, что к точкам системы
приложены силы
![]() .
Чтобы вычислить обобщенную силу, дадим
координате q1
ничтожно малое приращение q1
, оставляя прочие координаты без
изменения. Это изменение координаты q1
вызовет ничтожно малые перемещения 1,
2, п
всех точек системы.
Вычислим сумму работ сил
.
Чтобы вычислить обобщенную силу, дадим
координате q1
ничтожно малое приращение q1
, оставляя прочие координаты без
изменения. Это изменение координаты q1
вызовет ничтожно малые перемещения 1,
2, п
всех точек системы.
Вычислим сумму работ сил
![]() на перемещениях 1,
2,
п:
на перемещениях 1,
2,
п:
![]() .
.
Пусть эта работа равна произведению некоторого множителя Q1 на приращение координаты q1. Поступая аналогично, найдем Q2, … Qk, соответствующие координатам q2, … qk:
![]() .
.
Обобщенная сила – это величина, равная коэффициенту при приращении обобщенной координаты в выражении полной элементарной работы действующих на систему сил.
Не следует считать, что обобщенная сила всегда имеет размерность Ньютон. Работа всегда вычисляется в джоулях (1 Дж =1 Нм).
-
Размерность обобщенной координаты
Размерность обобщенной силы
м
Н
рад
Нм
м3
Па
В механической системе с идеальными связями обобщенные реакции связей всегда равны нулю, поэтому при переходе к обобщенным силам реакции связей автоматически выпадают из расчетов. В этом большое преимущество методов Лагранжа.
Примеры вычисления обобщенной силы
К барабану 1 радиуса R приложен момент М, под действием которого осуществляется подъем груза 2. Массы барабана и груза соответственно равны т1 и т2.

Представленная на рисунке механическая система имеет одну степень свободы. Для определения обобщенной силы выберем в качестве обобщенной координаты угол поворота барабана – (направим его против часовой стрелки). Дадим обобщенной координате приращение и вычислим полную элементарную работу всех активных сил на этом перемещении:
![]() .
.
Работа от веса барабана
равна нулю, т.к. ось его вращения не
перемещается. Тогда обобщенная сила
равна
![]() .
.
Другой пример.
Пусть система материальных точек М1,
М2, М3, … Мп
имеет k степеней
свободы. Обозначим ее обобщенные
координаты q1,
q2, … qk.
Возьмем декартовы оси x,
y, z
и обозначим координаты точки Мi
через
![]() .
Координаты являются функциями обобщенных
координат и времени:
.
Координаты являются функциями обобщенных
координат и времени:
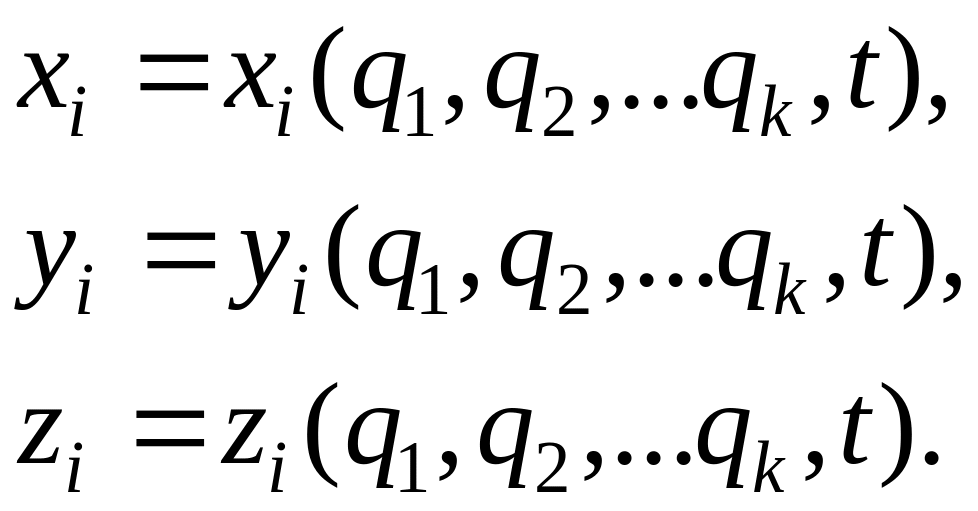
К системе приложены
силы
![]() .
Вычислим обобщенные силы
.
Вычислим обобщенные силы
![]() .
Например,
.
Например,
![]() .
.
Элементарную работу силы Fi мы можем вычислить как
![]() .
.
Т.к.
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
.
Рассуждая аналогично и поделив обе части равенства на q, получим:
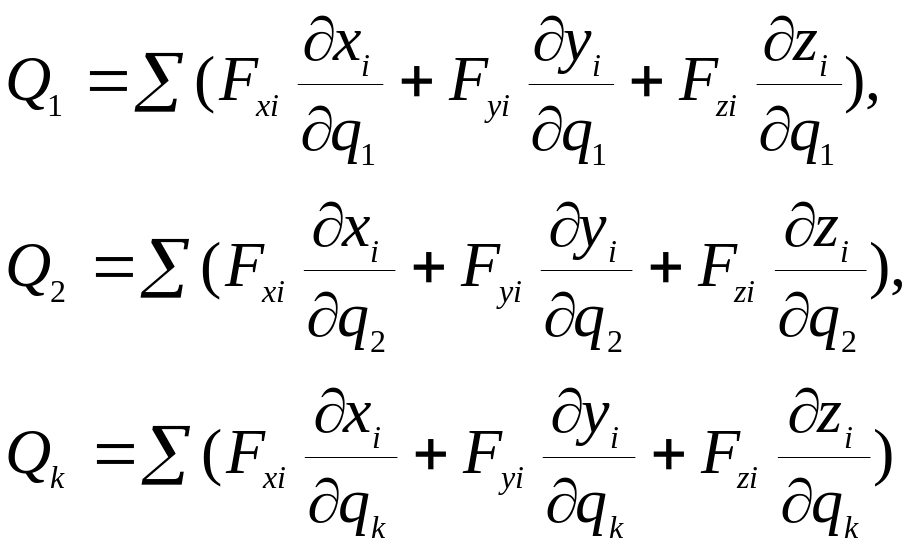
или
![]() .
.
