Динамические реакции, действующие на ось вращающегося тела

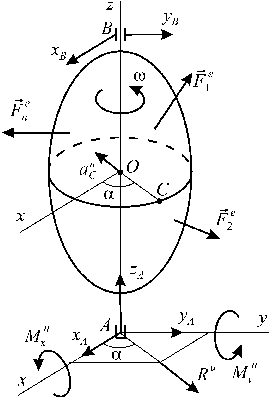
Пусть твердое тело вращается равномерно вокруг оси Оz в подшипниках А и В. Пусть координатные оси Аxyz вращаются вместе с телом. На тело действуют силы . Их равнодействующая имеет проекции , а их главные моменты – .

При этом , т.к.  = const.

Для определения динамических реакций подшипников x_A, y_A, z_A, x_B, y_B, z_В присоединим к заданным силам и реакциям силы инерции всех частиц тела и приведем их к точке А. Таким образом, получим:

Согласно принципу Даламбера, составим уравнения равновесия, полагая, что АВ = b:

, т.к. и .

Главный вектор сил инерции . При равномерном вращении возникает лишь нормальное ускорение , где h_С  – расстояние от точки С до оси вращения. Проецируем на оси координат, учитывая что h_С cos = x_С, получим:

h_С sin = y_С,

где x_С и y_С – координаты центра тяжести.

Тогда .

Чтобы определить и , рассмотрим частицу тела, удаленную от оси на расстояние h_С, тогда

.

Для всех точек тела

,

где и – центробежные моменты инерции.

Подставим найденные значения в написанную систему уравнений:

Эти уравнения определяют динамические реакции, действующие на ось, равномерно вращающуюся вокруг оси Оz твердого тела. Если  = 0, то получим статические реакции. Очевидно, что динамические реакции могут быть значительно больше статических. Причем они зависят от , x_С, y_С, J_xy, J_yz. Однако, если центр тела будет лежать на оси вращения, то x_С = 0, y_С = 0, J_xz = 0, J_yz = 0, тогда, если ось вращения будет главной центральной осью инерции тела, динамические реакции будут равны статическим.

Итак, если тело вращается вокруг одной из главных центральных осей тела, то динамические реакции равны статическим.

Центробежные моменты характеризуют степень динамической неуравновешенности тела. Динамическое уравновешивание является важной технической задачей.

Известно, что любое тело имеет по крайней мере три взаимно перпендикулярные главные центральные оси инерции. Любую ось, проведенную в теле, можно сделать главной центральной осью инерции прибавлением к телу двух точечных масс. Такой метод уравновешивания широко используется в технике. При этом окончательная балансировка проводится на специальных стендах.

Лекция 14 принцип возможных перемещений. Принцип даламбера – лагранжа (общее уравнение динамики)

Классификация связей. Принцип возможных перемещений. Число степеней свободы. Идеальные связи. Общее уравнение динамики

Связями называются ограничения, которые налагаются на положения и скорости точек механической системы и которые выполняются независимо от того, какие на систему действуют силы.

Классификация связей

С тационарные связи не изменяются со временем. Нестационарные связи изменяются со временем (пример нестационарной связи показан на рисунке). Геометрические связи накладывают ограничения на положение (координаты).

Кинематические (дифференциальные) связи ограничивают скорость. Обычно кинематическая связь является одновременно и геометрической, т.к. скорость является первой производной от координаты по времени. Если дифференциальную связь можно представить как геометрическую, т.е. зависимость между скоростями можно свести к зависимости между координатами, то такая связь называется интегрируемой, в противном случае – неинтегрируемой.

Геометрические и интегрируемые дифференциальные связи называются голономными, а неинтегрируемые – неголономными. Механические системы также делятся по виду связей на голономные и неголономные.

Пример. Колесо катится по рельсу, при этом V_C = R, . Проинтегрировав, получим x_С = R , следовательно, связь является голономной. Она также является геометрической, кинематической, дифференциальной и интегрируемой.

Удерживающие (двусторонние) связи препятствуют перемещению точек в противоположных направлениях. Неудерживающие (односторонние) связи препятствуют перемещению точек в одном направлении.

Пример.