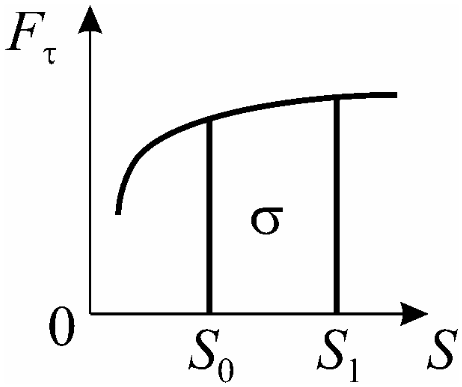
Графический способ вычисления работы

.

Геометрический смысл работы – площадь, ограниченная осью S, кривой F_ (S) и ординатами силы F_.

Мощность

Мощностью называется величина, равная работе, совершенной в единицу времени.

.

Мощность равна произведению касательной составляющей силы на скорость.

Если работа совершается равномерно, то .

Единица измерения мощности – 1 Ватт = 1 Дж/с. В технике используется также единица, называемая лошадиной силой (л.с.): 1 л.с. = 736 Вт.

Для измерения работы в технике широко используется единица, называемая киловатт-часом: 1 кВт∙ч = 3,6·10⁶ Дж.

Из равенства N = F∙V видно, что при движении в гору автомобиль, развивая ту же мощность, может увеличить силу тяги, уменьшив скорость, поэтому и включают пониженную передачу.

Примеры вычисления работы

1. Работа силы тяжести. Пусть точка М под действием силы тяжести перемещается из положения М₀ в положение М₁.

Если М₀ выше М₁, то z₀ – z₁ = h, где h – вертикальное перемещение точки, если точка перемещается вверх, то z₀ – z₁ = – h, следовательно, .

Работа силы тяжести не зависит от траектории движения точки, т.е. сила тяжести является потенциальной.

2. Работа силы упругости. Рассмотрим груз М, лежащий на плоскости и прикрепленный к свободному концу пружины.

Обозначим: – длина свободной пружины, – длина растянутой пружины, – удлинение пружины.

Т.к. , a (по закону Гука), то

.

Этот же результат можно получить графически.

Работа силы упругости равна половине произведения коэффициента жесткости на разность квадратов начального и конечного удлинений.

Формула справедлива и тогда, когда перемещение груза не является прямолинейным, т.е. не зависит от траектории, следовательно, сила упругости тоже является потенциальной.

3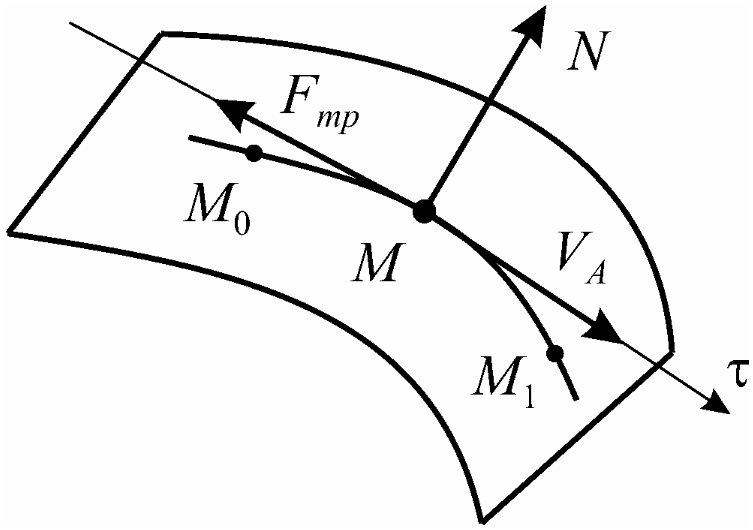 . Работа силы трения. Пусть точка движется по шероховатой поверхности по кривой М₀ М₁. Известен коэффициент трения _тр.

Поскольку ,

где N – нормальная реакция поверхности, то

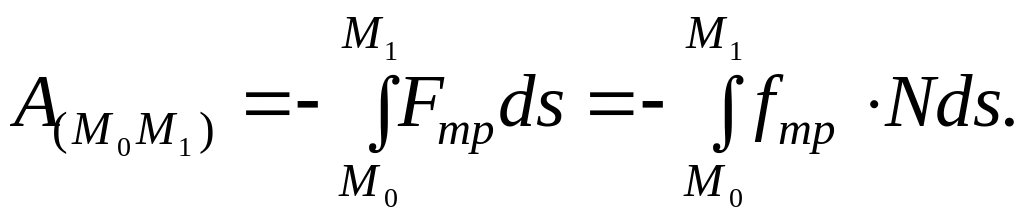
Если сила трения постоянна, то

,

где S – длина дуги кривой.

Таким образом, работа силы трения скольжения всегда отрицательна. Т.к. сила трения зависит от длины дуги (от траектории), то является непотенциальной.

Кинетическая энергия точки

Кинетической энергией (КЭ) материальной точки называется скалярная величина , равная половине произведения массы точки на квадрат скорости.

Единица измерения КЭ – 1 Джоуль (та же, что и для измерения работы).

Пусть точка массой m перемещается из положения М₀ со скоростью V₀ в положение М₁, где ее скорость будет V₁.

Известно, что m∙a = F_k . Проецируя равенство на ось , получим .

Представим тангенциальное ускорение в виде:

.

Тогда ,

следовательно, .

Проинтегрировав это выражение в пределах от М₀ до М₁ , получим

.

Изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении. Эту теорему называют теоремой об изменении кинетической энергии точки в конечном виде.

При несвободном движении точки в правую часть равенства войдет работа заданных сил и реакций связей.