Лекция 6 плоскопараллельное движение твердого тела (определение скоростей)

Разложение плоского движения твердого тела на поступательное и вращательное. Уравнение плоского движения. Определение скоростей точек твердого тела. Теорема о скоростях точек твердого тела, ее следствие. Определение скоростей точек твердого тела с помощью мгновенного центра скоростей. План скоростей

Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости.

Разложение плоского движения твердого тела на поступательное и вращательное

Плоское движение совершают многие части механизмов и машин (кривошипно-ползунный механизм, колесо, катящееся по рельсу, и т.п.). Для изучения движения всего тела достаточно изучить, как движется в плоскости xOz сечение S этого тела.

Положение фигуры S в плоскости xOz определяется положением какого-нибудь отрезка AB, проведенного на этой фигуре. В свою очередь, положение отрезка AB можно определить, зная координаты . Точку , выбранную для определения положения фигуры , будем называть полюсом.

Закон плоского движения фигуры имеет вид:

, , .

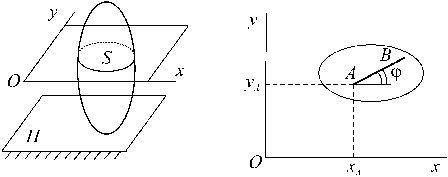
Это уравнения движения плоской фигуры в ее плоскости. Первые два уравнения определяют поступательное движение полюса (при ), а третье уравнение – вращательное движение фигуры вокруг полюса , .

Следовательно, движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса.

Кинематическими характеристиками такого движения будут ,  и .

В качестве полюса можно выбрать любую точку фигуры, например, C и определить положение фигуры отрезком СД. Характеристика поступательного движения изменится, так как в общем случае и (иначе движение было бы поступательным). Характеристики вращательной части движения ( и ) остаются неизменными, так как ₁ = – , где  = const. Поэтому .

За полюс принимается точка, скорость которой либо задана, либо ее легко определить из условия задачи.

Вращательная часть движения от выбора полюса не зависит.

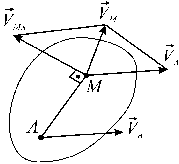
Определение скоростей точек твердого тела

Пусть оси движутся вместе с точкой A, оставаясь параллельными осям xOy. Тогда положение точки M будет определяться радиус-вектором :

,

где .

Тогда скорость точки определяется выражением

.

В полученном равенстве – скорость полюса A, – скорость, которую точка M получает при , то есть при вращении плоской фигуры относительно точки (полюса):

.

При этом , где – угловая скорость фигуры.

Теорема. Скорость любой точки М плоской фигуры геометрически складывается из скорости какой-нибудь другой точки А, принятой за полюс, и скорости, которую точка М получает при вращении фигуры вокруг этого полюса.

Модуль и направление скорости находятся путём построения параллелограмма.

Теорема о проекциях скоростей двух точек тела

Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу, то есть .

Доказательство. Разложим скорость на две составляющие в соответствии с равенством . Проецируя обе части равенства на ось, проходящую через точки и , получим

или