Частные случаи движения точки
1. Прямолинейное движение точки.
Траектория – прямая,
следовательно,
,
тогда
.
Поэтому полное ускорение равно
касательному
.
2. Равномерное движение точки.
Тогда
,
следовательно,
,
поэтому полное ускорение равно лишь
нормальному
.
3. Равномерное прямолинейное движение точки.
.
Из рассмотренных случаев видно, что касательное ускорение характеризует изменение величины (модуля) скорости, а нормальное – изменение направления скорости.
4. Равнопеременное движение.
За равные промежутки времени скорость изменяется на равные величины:
или
,
где
– скорость точки при
(начальная
скорость).
Так как
или
.
Интегрируя, получим
.
Лекция 5 простейшие движения твердого тела
Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращательное движение твердого тела вокруг неподвижной оси. Угловая скорость и угловое ускорение. Траектории, скорости и ускорения точек вращающегося твердого тела. Равномерное и равнопеременное вращение твердого тела. Определение скоростей и ускорений точек вращающегося тела
Поступательное движение твердого тела
Поступательным движением твердого тела называется такое движение, при котором отрезок прямой, соединяющий две любые точки тела, во все время движения остается себе параллельным (например, АВ).
Теорема. При поступательном движении твердого тела траектории, скорости и ускорения всех его точек одинаковы.
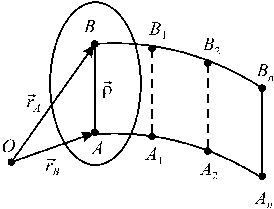
Доказательство.
Пусть отрезок АВ
тела за время
перемещается поступательно. Возьмем
произвольную точку O
и определим в пространстве положение
отрезка АВ
радиусами-векторами
и
.
Обозначим:
– радиус-вектор, определяющий положение
точки В
относительно точки А:
.
(1)
Вектор
не изменяется ни по величине, ни по
направлению, так как
(по определению поступательного
движения). Из соотношения (1) видно, что
траектория точки В получается из
траектории точки А параллельным
смещением точек этой траектории на
постоянный вектор
.
Таким образом, траектории точек А
и В будут одинаковыми.
Возьмем производную по времени от равенства (1). Тогда
,
т.е.
;
или
.
Следовательно, при поступательном движении твердого тела скорости и ускорения всех его точек в данный момент времени одинаковы.
Очевидно, что для изучения поступательного движения тела достаточно изучить движение какой-либо одной точки. Т.е. задача сводится к задаче кинематики точки, рассмотренной нами в предыдущей лекции.
Отметим, что сам факт поступательного движения не определяет ни закона движения, ни вида траектории. При поступательном движении точки тела могут описывать любые траектории (например, окружности). Но все они будут одинаковы.
Вращение твердого тела вокруг неподвижной оси
Если во все время движения твердого тела две какие-либо его точки остаются неподвижными, то такое движение тела называется вращением вокруг неподвижной оси, а прямая, проходящая через две неподвижные точки, называется осью вращения тела.
П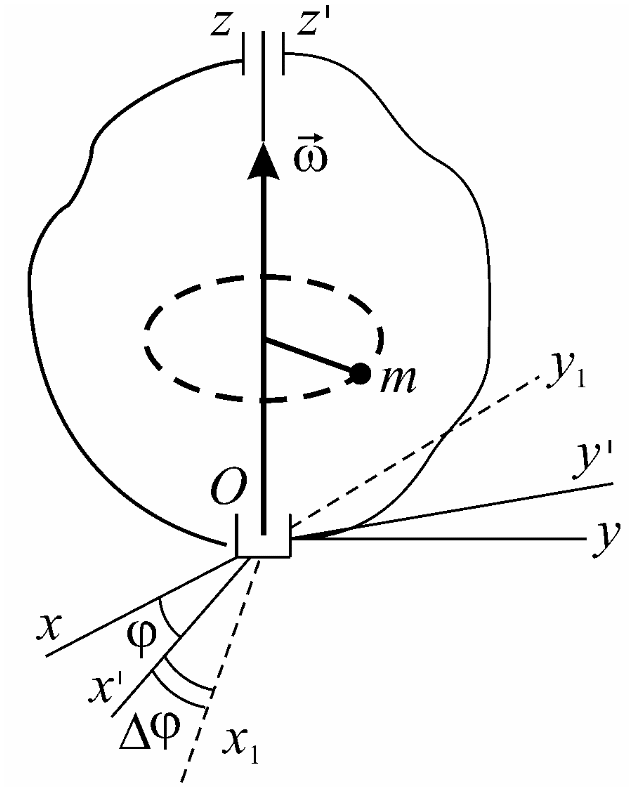
ри
таком движении тела все его точки, не
лежащие на оси вращения, будут описывать
окружности с центром на оси вращения
и с плоскостями, перпендикулярными
ей.
Выберем неподвижную систему координат Оxyz, ось Oz которой совпадает с осью вращения твердого тела. Возьмем также систему Оx'y'z', вращающуюся вместе с телом. Положение подвижной системы относительно неподвижной будет определяться двугранным углом между плоскостями с xOz и x'Oz'. Обозначим его . Угол изменяется с течением времени и представляет собой некоторую непрерывную функцию времени t. Таким образом, закон вращательного движения твердого тела имеет вид:
.
За положительное направление примем направление против часовой стрелки, если смотреть со стороны положительного направления оси Oz.