Векторно-координатный способ задания движения

Пусть закон движения задан радиус-вектором или равносильной ему системой трех скалярных координат:

.

Допустим, в некоторый момент времени t положение точки m определяет , а в следующий момент соответственно , тогда за время радиус-вектор получит приращение ' .

Вектор ' называется вектором перемещения точки за . Отношение вектора перемещения точки к соответствующему промежутку времени называется вектором средней скорости точки за промежуток времени :

И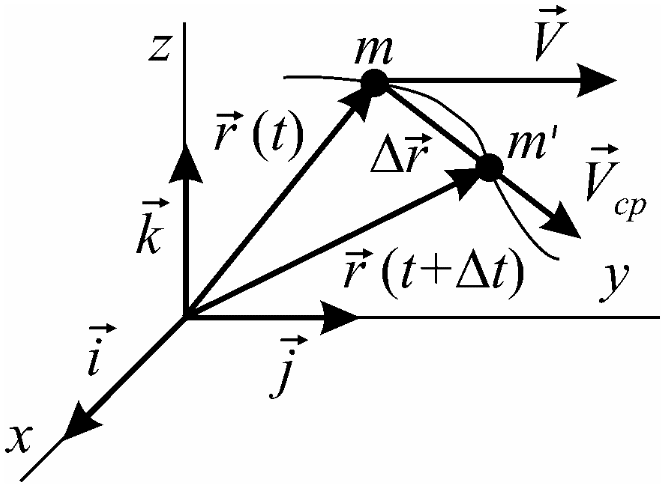 з уравнения следует, что – вектор, направленный по хорде в сторону движения. Очевидно, чем меньше , тем точнее будет выражать скорость точки в момент времени . Поэтому переходим в равенстве к пределу при Δt → 0.

– векторная производная.

Скорость точки равна векторной производной от радиус-вектора точки по времени и направлена по касательной к ее траектории в сторону движения:

или

,

где – проекции вектора скорости на координатные оси.

При этом

Складывая составляющие скорости, пролучим .

Таким образом, если движение точки задано системой уравнений (1), можно найти величину и направление скорости.

Естественный способ задания движения

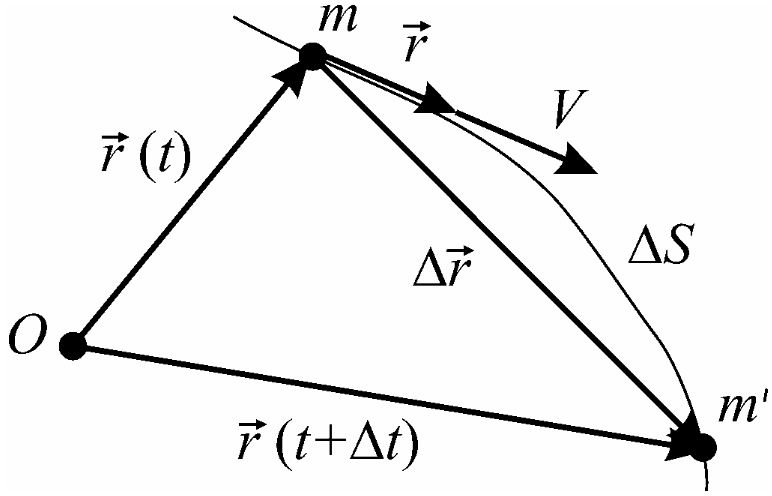
Пусть движение точки m задано уравнением . Требуется найти скорость точки. Пусть точка m определяется еще и радиус-вектором относительно точки O, тогда

.

Т.к. при , , то можно записать

.

Рассмотрим каждый предел в отдельности.

.

Предел отношения направляющей хорды к стягивающей ею дуге по величине равен единице и направлен по касательной к траектории: (r = 1), тогда , а алгебраическая величина скорости .

Единичный вектор направлен всегда в сторону возрастания дуговой координаты, поэтому при движении точки в сторону возрастания , а при движении в обратную сторону – .

Скорость точки равна первой производной от дуговой координаты по времени и направлена по касательной к траектории точки в сторону ее движения.

Определение ускорения точки при различных способах задания движения

Мера быстроты изменения скорости называется ускорением.

Векторно-координатный способ задания движения

Пусть движение точки m задано уравнением или системой уравнений

Е сли в момент времени t точка m имеет скорость , то в следующий момент ее скорость – .

Тогда .

Перенесем вектор из точки m' в точку m и построим параллелограмм. Тогда будет его стороной. Отношение приращения к промежутку времени называется средним ускорением точки m за время :

.

Очевидно, что вектор направлен по вектору . Ускорением точки в данный момент времени t называется предел, к которому стремится вектор среднего ускорения при :

.

Ускорение точки равно производной от вектора ее скорости по времени. Вспомнив, что , получим .

Чтобы найти величину и направление вектора ускорения аналитически, представим радиус-вектор через его проекции:

.

Тогда или .

Сравнивая эти равенства, получим:

Естественный способ задания движения точки. Понятие о естественном трехграннике

П остроим к кривой АВ в точке M касательную, единичный вектор которой обозначим через . Перпендикуляр к касательной называется нормалью. Очевидно, их может быть бесконечно большое число. Все они будут лежать в плоскости, проходящей через точку M, и будут перпендикулярны касательной. Это нормальная плоскость к кривой в данной точке. Нормаль, лежащая в соприкасающейся плоскости (плоскости кривой), называется главной нормалью, ее единичный вектор направлен в сторону вогнутости кривой АВ. Нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью, ее единичный вектор обозначим как . Плоскость Мb называется спрямляющей плоскостью. Три взаимно перпендикулярные оси, имеющие начало в точке M и направленные по векторам , , называются естественными или натуральными осями координат (оси естественного трехгранника). Такая система будет подвижной, так как при движении точки M начало координат и направление осей изменяется.

Пусть точка M движется по некоторой траектории , лежащей в соприкасающейся плоскости. Найдем проекции ускорения на нормаль и касательную к траектории. Обозначим: – проекция приращения вектора скорости на касательную, а – проекция на нормаль. Пусть точка движется из положения M в положение M' и в этих точках имеет скорости и , тогда .

Тогда – касательное ускорение,

– нормальное ускорение.

Перенесем вектор в точку M, при этом .

При также стремится к нулю, а фигура АDBC стремится к прямоугольнику, в котором диагональ АВ стремится к АС. Так как , , то . Но АС – проекция на касательную, то есть , тогда , следовательно, .

Далее, – это проекция на нормаль, то есть можно рассматривать как элементарную дугу радиуса MA, тогда и, следовательно, .

Угол между касательной и кривой в двух ее точках называется углом смежности, – элементарный угол смежности, тогда , где – радиус кривизны траектории, тогда

.

Тангенциальное (касательное) ускорение (проекция ускорения точки на касательную) равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) по времени. Нормальное (центростремительное) ускорение (проекция ускорения на главную нормаль) равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой.

Пусть точка M движется по кривой. Изобразим векторы . Вектор нормального ускорения всегда направлен в сторону вогнутости кривой. Вектор направлен по касательной к траектории как в сторону скорости (ускоренное движение), так и противоположно ей (замедленное движение).

Полное ускорение точки: