
- •Тр: “алгебра и аналитическая геометрия”
- •Задача 8. Найти общее решение и фундаментальную систему решений
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •12. Какую тройку (левую или правую) образуют векторы ,
- •Вариант 13
- •Вариант 14
- •14. Написать уравнение плоскости, проходящей через ось и точку
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •11. Найти единичный вектор, перпендикулярный векторам и
- •Вариант 21
- •11. Найти единичный вектор, перпендикулярный векторам и
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •14. Написать уравнение плоскости, проходящей через ось и точку
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
Тр: “алгебра и аналитическая геометрия”
Задача 1. Вычислить определитель.
Задача 2. Даны
матрицы
![]() и
и
![]() .
Найти матрицу
.
Найти матрицу
![]() .
.
Задача 3. Найти
произведение матриц
![]() .
Существует ли
.
Существует ли
произведение
![]() ?
Почему?
?
Почему?
Задача 4. Найти обратную матрицу для матрицы . Сделать проверку.
Задача 5. Решить матричное уравнение.
Задача 6. Найти ранг матрицы.
Задача 7. Решить систему линейных уравнений:
по формулам Крамера;
с помощью обратной матрицы;
методом Гаусса.
Задача 8. Найти общее решение и фундаментальную систему решений
для системы уравнений.
Задача 9. Написать
разложение вектора
![]() по векторам
по векторам
![]() ,
,
![]() и
и
![]() .
.
Задача 10-16. Условия приведены в задании.
Вариант 1
1.
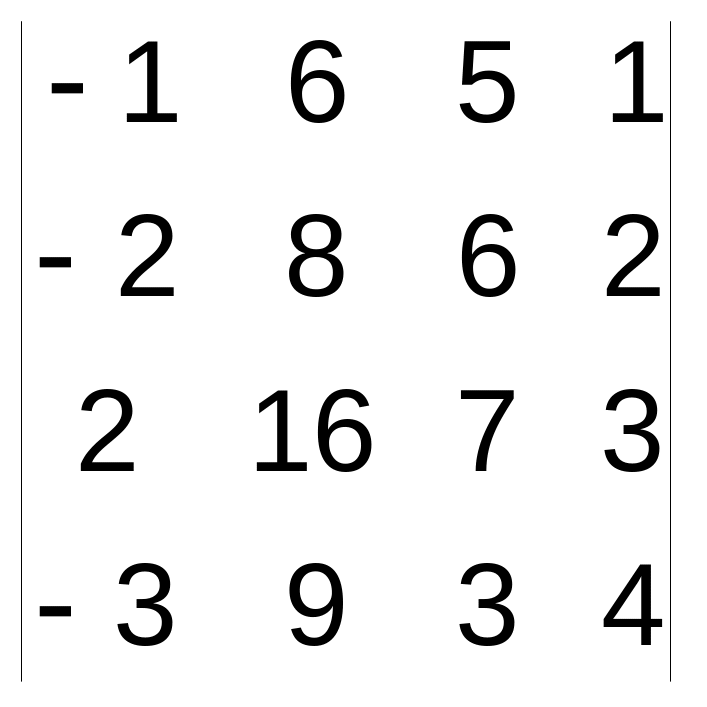 2.
2.
![]() ,
,
 ,
,
![]()
3.
![]() ,
,
 4.
4.
 5.
5.
![]()
6.
 7.
7.
![]() 8.
8.
![]()
9.
![]() ,
,
![]() ,
,
![]() и
и
![]()
10.
Вычислить проекцию вектора
![]() на направление вектора
на направление вектора![]() ,
,
где
![]() ;
;
![]() .
.
11.
Векторы
![]() и
и
![]() образуют угол в
образуют угол в
![]() ,
,
![]() ,
,
![]() .
Найти длину
.
Найти длину
вектора
![]() ,
если
,
если
![]() .
.
12.
Лежат ли точки
![]() ,
,
![]() ,
,
![]() и
и
![]() в одной
в одной
плоскости?
13. Составить уравнения сторон треугольника, зная одну из его вершин
![]() и уравнения двух
высот:
и уравнения двух
высот:
![]() и
и
![]() .
.
14.
Написать уравнение плоскости, проходящей
через ось
![]() и точку
и точку
![]() .
.
15.
Составить уравнение прямой, которая
проходит через точку
![]()
перпендикулярно
к вектору
![]() и пересекает прямую
и пересекает прямую
![]() .
.
16.
Принадлежит ли прямая
![]() плоскости
плоскости
![]() ?
?
Вариант 2
1.
 2.
2.
 ,
,
 ,
,
![]()
3.
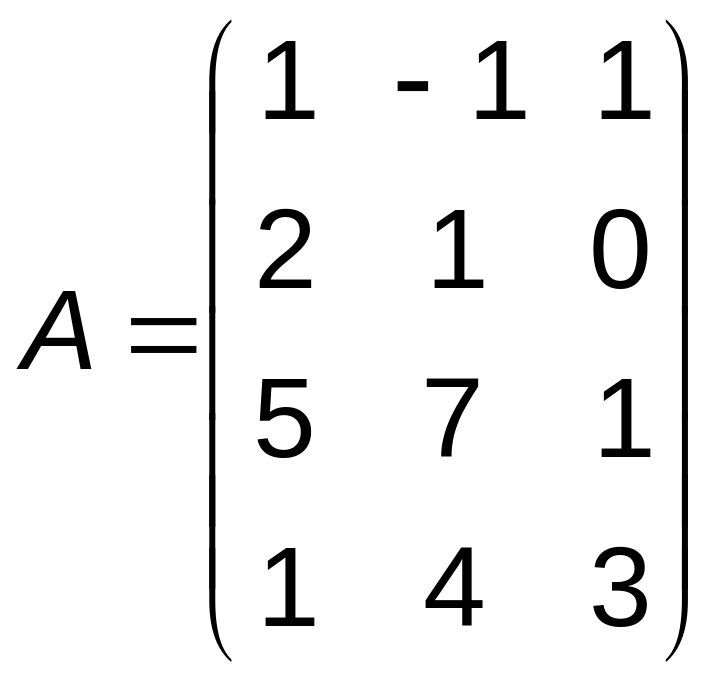 ,
, 4.
4. 5.
5.![]()
6.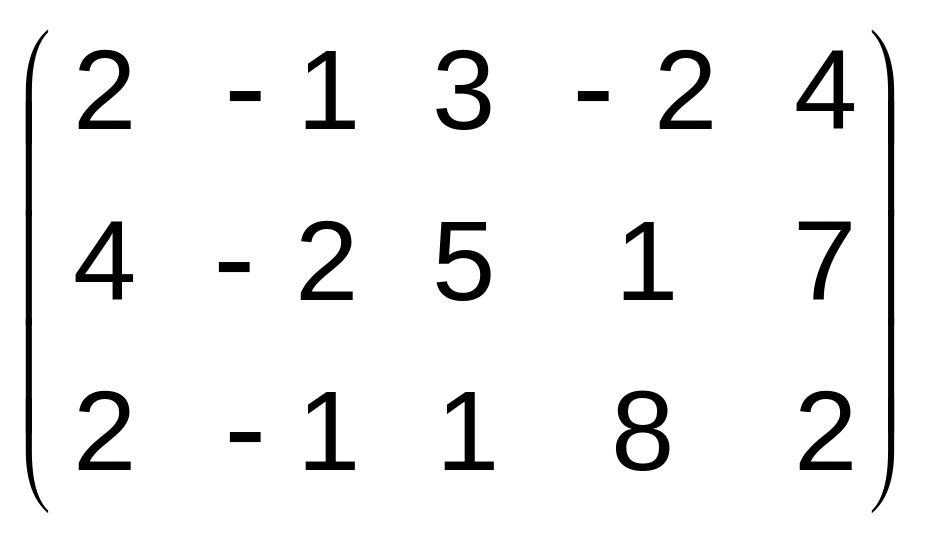 7.
7. 8.
8.![]()
9.
![]() ,
,
![]() ,
,
![]() и
и
![]()
10.
Найти единичный вектор, перпендикулярный
векторам
![]() и
и
![]() .
.
11.
Сила
![]() приложена к точке
приложена к точке
![]() .
Определить момент
.
Определить момент
этой силы
относительно точки
![]() .
.
12.
Какую тройку (левую или правую) образуют
векторы
![]() ,
,
![]() и
и
![]() ?
?
13.
Составить уравнения
сторон треугольника, зная одну его
вершину
![]() ,
,
а также уравнения
высоты
![]() и медианы
и медианы
![]() ,
,
проведенных из различных вершин.
14.
Написать уравнение плоскости, проходящей
через точку
![]() и
и
отсекающей от осей координат положительные и равные отрезки.
15.
Составить каноническое уравнение
прямой, лежащей в плоскости
![]() ,
,
проходящей через начало координат и перпендикулярной к прямой
![]() .
.
16.
Найти угол между прямой
![]() и плоскостью, проходящей
и плоскостью, проходящей
через точки
![]() ,
,
![]() ,
,
![]() .
.
Вариант 3
1.
 2.
2.
 ,
,
![]() ,
,
![]()
3.
![]() ,
,
 4.
4.
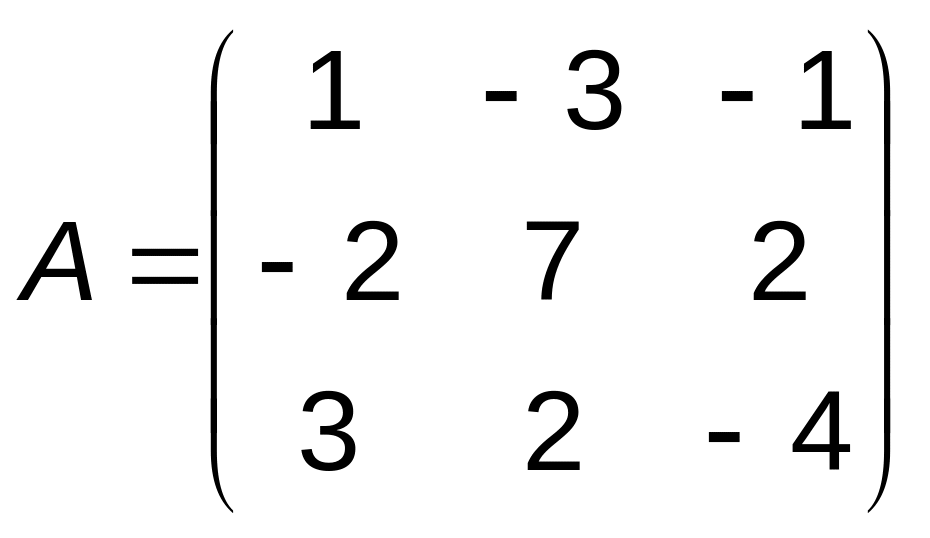 5.
5.
![]()
6.
 7.
7.
 8.
8.

9.
![]() ,
,
![]() ,
и
,
и
![]()
10.
При каком t
векторы
![]() и
и
![]() будут взаимно
будут взаимно
перпендикулярны?
11.
Вычислить площадь треугольника,
построенного на векторах
![]() и
и
![]() ,
если
,
если
![]() ,
угол между векторами
,
угол между векторами
![]() и
и
![]() равен
равен
![]() .
.
12.
Компланарны ли векторы
![]() ,
,
![]() и
и
![]() ?
?
13.
Через точку пересечения прямых
![]() и
и
![]() провести
провести
прямую, которая, кроме того, 1) проходит через начало координат;
2) параллельна оси абсцисс; 3) параллельна оси ординат;
4) проходит
через точку
![]() .
.
14. Написать уравнение плоскости, проходящей через точки М(1; 2; 0) и
N(2;
1; 1) параллельно вектору
![]() (3;
0; 1).
(3;
0; 1).
15. Составить уравнение прямой, проходящей через точку M (3; -2; 0) перпен-
дикулярно к
прямой
![]() и расположенной
в плоскости
и расположенной
в плоскости
![]() .
.
16. Составить уравнение прямой, проходящей через точки пересечения
плоскости
![]() с прямыми
с прямыми
![]() и
и
![]() .
.
