1.4.2 Определение равнодействующей аналитическим способом

Знать аналитический способ определения равнодействующей силы, условия плоской сходящихся системы сил в аналитической форме.

Уметь определять проекции силы на две взаимно перпендикулярные оси, решать задачи на равновесие в аналитической форме.

Проекция силы на ось

Проекция силы на ось определяется отрезком оси, отсекаемым перпендикулярами, опущенными на ось из начала и конца вектора (рис. 1.15).

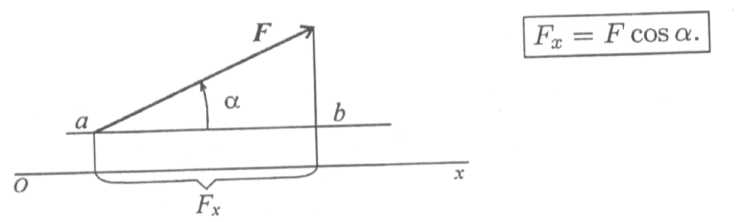
рис. 1.15

В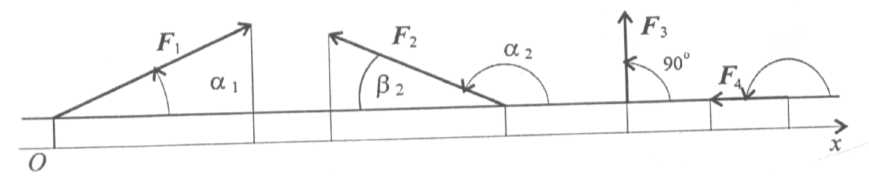 еличина проекции силы на ось равна произведению модуля си­лы на косинус угла между вектором силы и положительным напра­влением оси. Таким образом, проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси (рис. 1.16).

рис. 1.16

F_1x = F₁ cos α₁ > 0; F_2x = F₂ cos α₂ = - F₂ cos β₂;

cos α₂ = cos (180° - β₂) = - cos β₂;

F_3x = F₃ cos 90° = 0; F_4x = F₄ cos 180° = - F₄

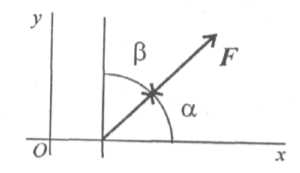
Проекция силы на две взаимно перпендикулярные оси

(рис. 1.17).

F_x = F cos a > 0;

F_y = F cos β = F sin α > 0. рис.1.17

Определение равнодействующей системы сил аналитическим способом

Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определяем равнодействующую геоме­трическим способом. Выберем систему координат, определим про­екции всех заданных векторов на эти оси (рис. 1.18а). Складываем проекции всех векторов на оси х и у (рис. 1.18б).

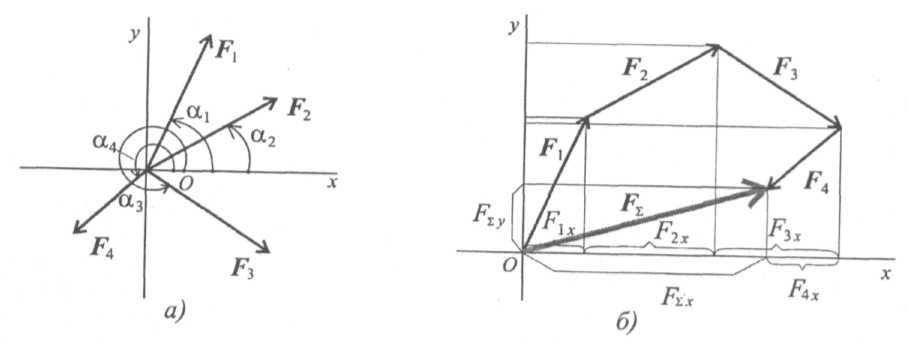
рис.1.18

F_Σч = F_lx + F_2x + F_3x + F_4x; F_Σн = F_ly + F_2y + F_3y + F_4y;

; . Модуль (величину) равнодействующей можно найти по известным проекциям:

. Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействую­щей с осями координат (рис. 1.19).

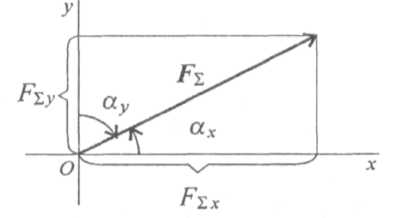
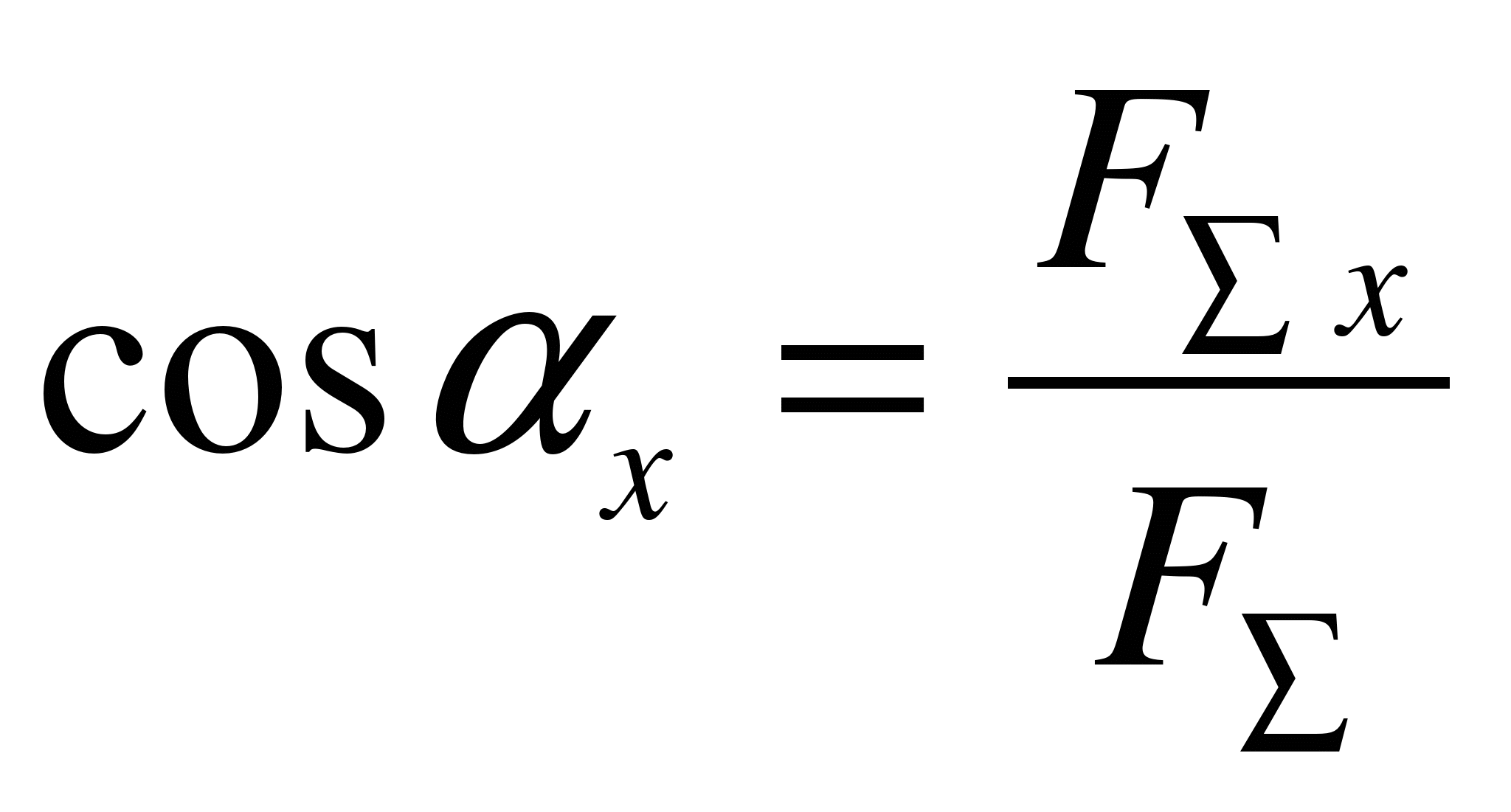
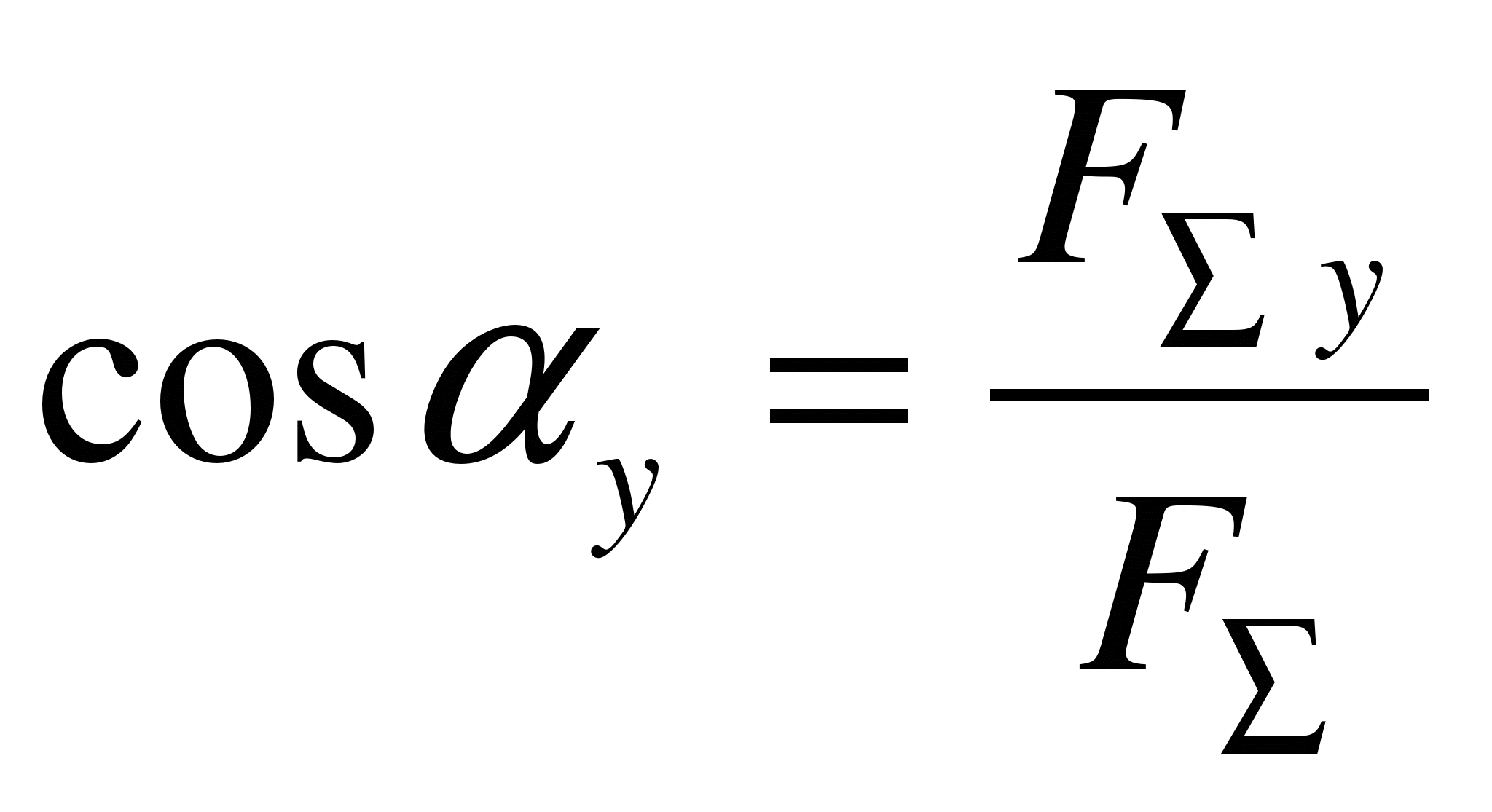
рис.1.19

Условия равновесия плоской системы сходящихся сил в аналитической форме

Исходя из того, что равнодействующая равна нулю, получим:

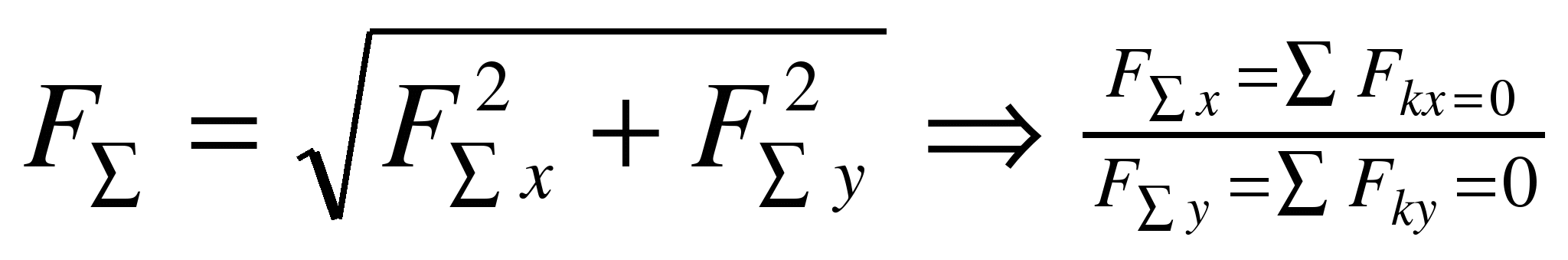
F_Σ = 0.

Условия равновесия в аналитической форме можно сформулиро­вать следующим образом:

Плоская система сходящихся сил находится в равновесии, ес­ли алгебраическая сумма проекций всех сил системы на любую ось равна нулю.

Система уравнений равновесия плоской сходящейся системы сил:

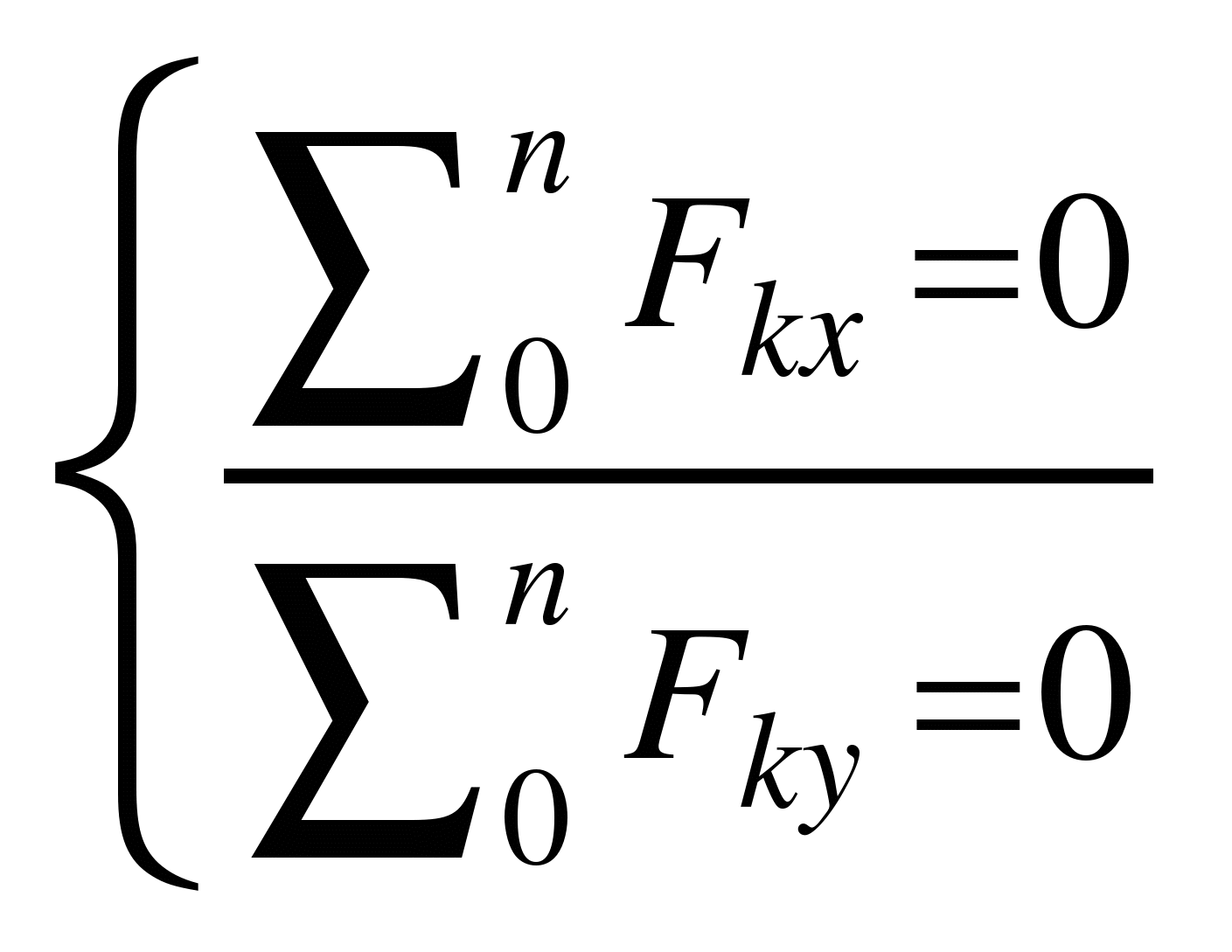
В задачах координатные оси выбирают так, чтобы решение было наиболее простым. Желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.

Методика решения задач

Решение каждой задачи можно условно разделить на три этапа.

Первый этап: Отбрасываем внешние связи системы тел, равновесие которой рассматривается, и заменяем их действие реакциями. Необходимость этого вызвана тем, что положения статики применимы только к свободным от внешних связей телами или системами тел.

Второй этап: Расчленяем систему тел на отдельные элементы. Это дает нам возможность определить внутренние силы (если это необходимо).

Третий этап: Составляем условия равновесия для каждого отдельного элемента, из которых находим искомые неизвестные величины и направления сил или реакций.

В зависимости от метода решения задач условия равновесия используется в геометрической или аналитической форме.