Какие векторы являются равными?

Два вектора равны, если они сонаправлены и имеют одинаковую длину. Заметьте, что сонаправленность подразумевает коллинеарность векторов. Определение будет неточным (избыточным), если сказать: «Два вектора равны, если они коллинеарны, сонаправлены и имеют одинаковую длину».

С точки зрения понятия свободного вектора, равные векторы – это один и тот же вектор, о чём уже шла речь в предыдущем параграфе.

Координаты вектора на плоскости и в пространстве

Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы   и  :

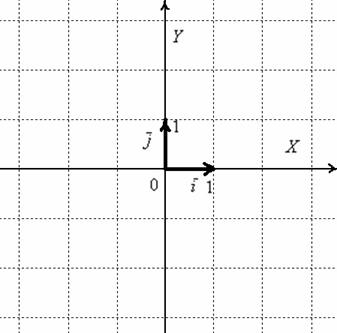
Векторы   и   ортогональны. Ортогональны = Перпендикулярны. Рекомендую потихоньку привыкать к терминам: вместо параллельности и перпендикулярности используем соответственно слова коллинеарность и ортогональность.  

Обозначение: ортогональность векторов записывают привычным значком перпендикулярности, например:  .

Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости. Что такое базис, думаю, интуитивно многим понятно, более подробную информацию можно найти в статье Линейная (не) зависимость векторов. Базис векторов. Простыми словами, базис и начало координат задают всю систему – это своеобразный фундамент, на котором кипит полная и насыщенная геометрическая жизнь.

Иногда построенный базис называют ортонормированным базисом плоскости: «орто» – потому что координатные векторы ортогональны, прилагательное «нормированный» означает единичный, т.е. длины векторов базиса равны единице.

Обозначение: базис обычно записывают в круглых скобках, внутри которых в строгой последовательности перечисляются базисные векторы, например:  . Координатные векторы нельзя переставлять местами.

Любой вектор   плоскости единственным образом выражается в виде: , где   – числа, которые называются координатами вектора в данном базисе. А само выражение   называется разложением вектора   по базису  .

Ужин подан:

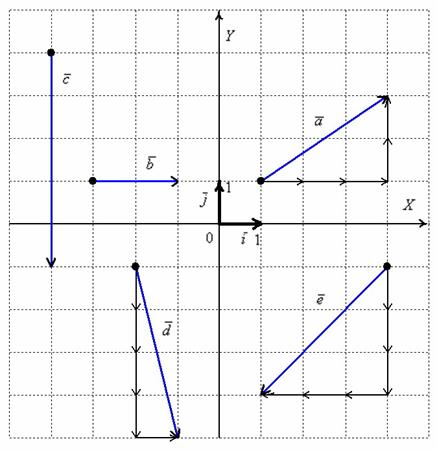
! ВСЕМ настоятельно рекомендую прочитать ВСЁ!

Начнем с первой буквы  алфавита: . По чертежу хорошо видно, что при разложении вектора по базису используются только что рассмотренные: 1) правило умножения вектора на число:   и  ; 2) сложение векторов по правилу треугольника:  .

А теперь мысленно отложите вектор   от любой другой точки плоскости. Совершенно очевидно, что его разложение   будет «неотступно следовать за ним». Вот она, свобода вектора – вектор «всё носит при себе». Это свойство, разумеется, справедливо для любого вектора. Забавно, что сами базисные (свободные) векторы   не обязательно откладывать от начала координат, один можно нарисовать, например, слева внизу, а другой – справа вверху, и от этого ничего не изменится! Правда, делать так не нужно, поскольку преподаватель тоже проявит оригинальность и нарисует вам «зачтено» в неожиданном месте.

Векторы  ,   иллюстрируют в точности правило умножения вектора на число, вектор   сонаправлен с базисным вектором  , вектор   направлен противоположно по отношению к базисному вектору  .  У данных векторов одна из координат равна нулю, дотошно можно записать так: А базисные векторы, к слову, так:   (по сути, они выражаются сами через себя).

И, наконец:  ,  . Кстати, что такое вычитание векторов, и почему я не рассказал о правиле вычитания? Где-то в линейной алгебре, уже не помню где, я отмечал, что вычитание – это частный случай сложения. Так, разложения векторов «дэ» и «е» преспокойно записываются в виде суммы:  ,  . Переставьте слагаемые местами и проследите по чертежу, как чётко в этих ситуациях работает старое доброе сложение векторов по правилу треугольника.

Рассмотренное разложение вида   иногда называют разложением вектора в системе орт (т.е. в системе единичных векторов). Но это не единственный способ записи вектора, распространён следующий вариант:

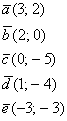 Или со знаком равенства: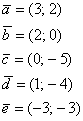 

Сами базисные векторы записываются так:   и 

То есть, в круглых скобках указываются координаты вектора. В практических задачах используются все три варианта записи.

Сомневался, говорить ли, но всё-таки скажу: координаты векторов переставлять нельзя. Строго на первом месте записываем координату, которая соответствует единичному вектору  , строго на втором месте записываем координату, которая соответствует единичному вектору  . Действительно,   и   – это ведь два разных вектора.

С координатами на плоскости разобрались. Теперь рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничусь одним вектором, который для простоты отложу от начала координат:

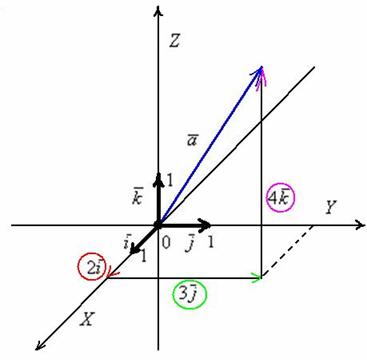
Перед вами ортонормированный базис   трехмерного пространства и прямоугольная система координат, единичные векторы   данного базиса попарно ортогональны:   и  . Ось   наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства. О том, как правильно выполнять плоские и трехмерные чертежи на клетчатой бумаге, читайте в самом начале методичкиГрафики и свойства функций.

Любой вектор   трехмерного пространства можно единственным способом разложить по ортонормированному базису  :  , где   – координаты вектора   (числа) в данном базисе.

Пример с картинки:  . Давайте посмотрим, как здесь работают правила действий с векторами. Во-первых, умножение вектора на число:   (красная стрелка),   (зеленая стрелка) и   (малиновая стрелка). Во-вторых, перед вами пример сложения нескольких, в данном случае трёх, векторов:  .  Вектор суммы   начинается в исходной точке отправления (начало вектора  ) и утыкается в итоговую точку прибытия (конец вектора  ).

Все векторы трехмерного пространства, естественно, тоже свободны, попробуйте мысленно отложить вектор   от любой другой точки, и вы поймёте, что его разложение    «останется при нём».

Аналогично плоскому случаю, помимо записи   широко используются версии  со скобками:   либо  .

Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры: вектор   (дотошно  ) – запишем  ; вектор   (дотошно  ) – запишем  ; вектор   (дотошно  ) – запишем  .

Базисные векторы записываются следующим образом:

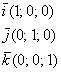
Вот, пожалуй, и все минимальные теоретические знания, необходимые для решения задач аналитической геометрии. Возможно многовато терминов и определений, поэтому чайникам рекомендую перечитать и осмыслить данную информацию ещё раз. Да и любому читателю будет полезно время от времени обращаться к базовому уроку для лучшего усвоения материала. Коллинеарность, ортогональность, ортонормированный базис, разложение вектора – эти и другие понятия будут часто использоваться в дальнейшем. Отмечу, что материалов сайта недостаточно для сдачи теоретического зачета, коллоквиума по геометрии, так как все теоремы (к тому же без доказательств) я аккуратно шифрую – в ущерб научному стилю изложения, но плюсом к вашему пониманию предмета. Для получения обстоятельной теоретической справки прошу следовать на поклон к профессору Атанасяну.    

А мы переходим к практической части: