Проекция вектора на вектор. Проекция вектора на координатные оси. Направляющие косинусы вектора

Рассмотрим векторы   и  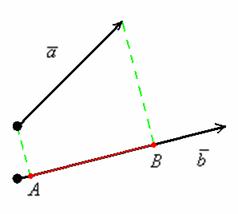: Спроецируем вектор   на вектор  , для этого из начала и конца вектора   опустимперпендикуляры на вектор   (зелёные пунктирные линии). Представьте, что на вектор   перпендикулярно падают лучи света. Тогда отрезок   (красная линия) будет «тенью» вектора  . В данном случае проекцией вектора    на вектор   является ДЛИНА отрезка  . То есть, ПРОЕКЦИЯ – ЭТО ЧИСЛО.

Данное ЧИСЛО обозначается следующим образом:  , «большим вектором» обозначают вектор КОТОРЫЙ проецируют, «маленьким подстрочным вектором» обозначают вектор НАкоторый проецируют.  

Сама запись   читается так: «проекция вектора «а» на вектор «бэ»».

Что произойдёт, если вектор «бэ» будет «слишком коротким»? Проводим прямую линию, содержащую вектор «бэ». И вектор «а» будет проецироваться уже на направление вектора «бэ», попросту – на прямую, содержащую вектор «бэ». То же самое произойдёт, если вектор «а» отложить в тридесятом царстве – он всё равно легко спроецируется на прямую, содержащую вектор «бэ».

Если угол между векторами   острый (как на рисунке), то 

Если векторы   ортогональны, то   (проекцией является точка, размеры которой считаются нулевыми).

Если угол между векторами   тупой (на рисунке мысленно переставьте стрелочку вектора  ), то   (та же длина, но взятая со знаком минус).

Отложим данные векторы от одной точки:

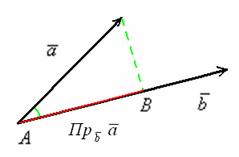
Очевидно, что при перемещении вектора его проекция не меняется

Вспомним школу. Рассмотрим прямоугольный треугольник. Косинусом острого угла называется отношение прилежащего катета к гипотенузе. В данном случае:

С другой стороны, у нас уже получена формула косинуса угла между векторами:

Таким образом:

Сокращаем знаменатели обеих частей на   и получаем формулу для вычисления проекции:

Формула выведена, распишем её в координатах:

Если векторы плоскости   и  , заданы в ортонормированном базисе  , то проекция вектора   на вектор   выражается формулой: .

Если векторы пространства  , заданы в ортонормированном базисе  , то проекция вектора   на вектор   выражается формулой:

Пример 18

Найти проекцию вектора   на вектор 

Решение в одну строчку:

Ответ: 

Проекция – это ДЛИНА, поэтому обязательно указываем размерность. Длина, конечно, своеобразная, в случае тупизны угла между векторами к ней добавляется знак «минус».

В задачах приходится находить не только проекцию вектора на вектор, но и проекцию отрезка на отрезок, отрезка на прямую и т.д. Но, так или иначе, в решении используются векторы!

Пример 19

Треугольник задан своими вершинами  . Найти: а) проекцию стороны   на сторону  ; б) проекцию стороны   на сторону  .

Это задача для самостоятельного решения. Решение и ответ в конце урока.

Выясним геометрический смысл координат векторов в ортонормированном базисе:

Проекция вектора на координатные оси. Направляющие косинусы вектора

Рассмотрим вектор плоскости  , заданный своими координатами в ортонормированном базисе  . Для удобства я отложу его от начала координат:

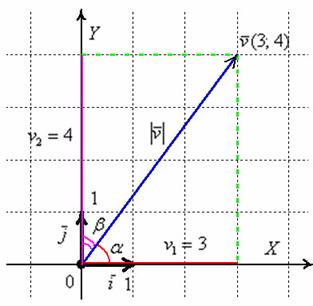
Проекцией вектора   на координатную ось   является в точности его первая координата:   (красная черта). Обозначим через   угол между вектором   и координатным вектором  :   (красная дуга). Тогда:  (определение косинуса в прямоугольном треугольнике недавно упоминалось).

Аналогично со второй координатой: проекцией вектора   на координатную ось   является его вторая координата:   (малиновая черта). Обозначим через   угол между вектором   и координатным вектором  :   (двойная малиновая дуга). Тогда:

Косинусы   называются направляющими косинусами вектора. Причём, для любого ненулевого вектора справедливо равенство  . Проверим его справедливость для рассматриваемого вектора: , что и требовалось проверить.

Заметьте, что приведённые выше выкладки не изменятся, если вектор   отложить от любой другой точки плоскости.

Итак, координаты вектора в ортонормированном базисе – это его проекции на направления соответствующих координатных векторов (координатные оси).

Направляющие косинусы ненулевого вектора  , заданного в ортонормированном базисе  , выражаются формулами  , а сами координаты вектора можно выразить через его длину и данные косинусы:  , то есть:  .

Кроме того, вектор с координатами из соответствующих направляющих косинусов:

– коллинеарен исходному вектору «вэ»;

– его длина равна единице (так называемый единичный вектор).

С пространственными векторами, заданными в ортонормированном базисе  ,  разборки точно такие же. Рассмотрим произвольный ненулевой вектор  . Его координаты представляют собой проекции вектора на оси   соответственно. Обозначим углы данного вектора с ортами через:  . Тогданаправляющие косинусы вектора выражаются формулами:  , и справедливым является равенство  .

В практических задачах чаще всего требуется найти направляющие косинусы вектора, заключительный пример урока:

Пример 20

Найти направляющие косинусы векторов: а)  , проверить, что  ; б)  , проверить, что  .

Простая задача для самостоятельного решения. Фактически, она состоит в том, чтобы найти длину векторов и составить эти самые направляющие косинусы. Однако не забывайте, что вместе с направляющими косинусами нам автоматически становятся известными единичные векторы, которые коллинеарны векторам «а» и «бэ». К слову, практическая задача на нахождения единичного вектора рассмотрена в Примере №5 урока Уравнение плоскости. Ну а здесь решение и ответ совсем близко.

После изучения данного урока, у вас уже весьма приличная подготовка по аналитической геометрии. Чтобы паззл сложился окончательно, читайте статьи Линейная (не) зависимость векторов. Базис векторов и Векторное и смешанное произведение векторов.

Любите векторы, и векторы полюбят вас!

Решения и ответы:

Пример 2: Решение:  Ответ: 

Пример 4: Решение:  Ответ: 

Пример 6: Решение:  Ответ: 

Пример 7*: Решение: Используем формулу  .  Найдём скалярное произведение: Найдём длину вектора  : Найдём длину вектора  : Таким образом: Ответ: 

Пример 10: Решение:  а) Найдем векторы: Вычислим скалярное произведение: , значит, прямые   не перпендикулярны. б) Найдем векторы: Вычислим скалярное произведение: , значит, прямые   перпендикулярны. Ответ: а) прямые   не перпендикулярны, б) 

Пример 12: Решение: Составим и решим уравнение: Ответ: при 

Пример 14: Решение:  Ответ: 

Пример 17: Решение: Найдем векторы  Вычислим косинус угла: Угол:  Ответ: 

Пример 19: Решение: Найдём векторы: Ответ: 

Пример 20: Решение:  а) Найдём длину вектора:  . Направляющие косинусы:  . Проверка:  , что и требовалось проверить. б) Найдём длину вектора:  . Направляющие косинусы:  . Проверка:  , что и требовалось проверить.

Ответ: 

Автор: Емелин Александр