2.2.2. Методи сліпого пошуку
Найбільш типовими алгоритмами сліпого перебору є:
повний перебір;
алгоритм рівних цін;
алгоритм перебору вглиб.
Алгоритм повного перебору
Вершини розкриваються у тому порядку, у якому вони були породжені. Першою розкривається початкова вершина. Перевіряється, чи немає серед породжених вершин цільової. Якщо є, то пошук закінчується. Якщо ні,то розкривається перша з породжених і перевіряється наявність цільових вершин.
Для структурованого запису алгоритму введемо поняття переліку відкритих і закритих вершин.
Перелік закритих вершин (ЗКР) – перелік, що містить ідентифікатори розкритих вершин і вершини, яку зараз належить розкрити. Вершини зі списку ЗКР, крім останньої, розкривати не можна.
Перелік відкритих вершин (ВДК) – перелік, де розміщують вершини, які можуть і повинні бути розкриті.
Алгоритм рівних цін.
Нехай кожній дузі поставлена у відповідність певна функція вартості Сij. Треба знайти шлях мінімальної вартості. Розкриття вершин здійснюється в порядку зростання їх вартості. Позначимо g(v) – вартість розкриття деякої вершини v і опишемо алгоритм рівних цін.
1.Поміститити початкову вершину S0 у перелік ВДК. Покласти g (S0)=0.
2.Якщо перелік ВДК порожній, то подати сигнал про невдачу пошуку, в іншому випадку перейти до наступного кроку.
3.Взяти з переліку ВДК ту вершину, для якої величина g(v) має найменше значення і помістити її в перелік ЗКР. Присвоїти цій вершині ідентифікатор v (якщо вершин з мінімальною декілька, то можна обрати будь-яку з них).
4.Якщо v є цільовою вершиною, то видати вирішальний шлях, інакше перейти до наступного кроку.
5.Розкрити вершину v . Для кожної дочірньої вершини vi вирахувати вартість g(vi) за формулою g= g+c(. Помістити ці вершини разом з відповідними їм g у перелік ВДК і побудувати вказівники, що йдуть від них до вершини . Якщо вершина не має дочірніх вершин, то перейти відразу до кроку 2.
6.Перейти до кроку 2.
Алгоритм рівних цін є узагальненням алгоритму повного перебору і зводиться до нього за умови, що вартості розкриття усіх вершин рівні.
Алгоритм перебору в глибину
Визначимо глибину вершини числом, що дорівнює номеру її рівня.
При переборі в глибину завжди розкривається та з вершин, що має найбільшу глибину.
Оскільки декілька вершин можуть мати однакову глибину, передбачається, що є правило обрання однієї з них.
Крім того, задається гранична глибина, вершини, що мають глибину, яка дорівнює граничній, не розкриваються.
Алгоритм:
1.Помістити початкову вершину у перелік ВДК.
2.Якщо перелік ВДК порожній, то видається повідомлення про невдачу, інакше перейти до кроку 3.
3.Взяти першу вершину зі списку ВДК і перенести в список ЗКР. Цій вершині присвоїти ідентифікатор.
4.Якщо глибина вершини v дорівнює граничній глибині, то перейти до 2, інакше до 5.
5.Розкрити вершину v. Помістити усі дочірні вершини на початок переліку ВДК і побудувати вказівники, що йдуть від них до вершини v. Якщо v не має дочірніх вершин, то перейти до кроку 2.
6.Якщо одна з цих вершин цільова, то на вихід видати рішення, що отримується шляхом перегляду назад у відповідності з вказівниками, інакше перейти до кроку 2.
Рис.2.5. Граф алгоритму перебору в глибину
Один з можливих графів алгоритму перебору в глибину
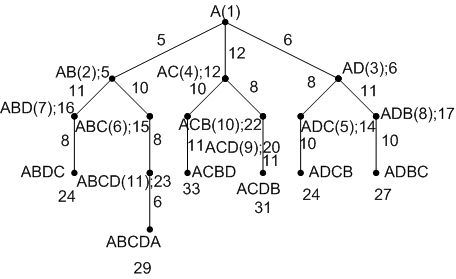
Рис.2.6. Граф алгоритму перебору в глибину
Граф про обрання маршруту алгоритму рівних цін.
В () – номер розкриття вершини, через ; - вага пройденого шляху
g= g+c(
Після кожного кроку розкриття вершини здійснюється перевпорядкування вершин у переліку у відповідності зі значенням оціночної функції.
Процедури такого типу – алгоритми впорядкованого перебору.