
- •1.Матрицы, действия над матрицами. Свойства действий.
- •2.Определители второго порядка. Алгебраические дополнения и миноры.
- •3.Определители третьего порядка. Вычисление по правилу треугольника.
- •4.Определитель п-ого порядка, его свойства. Вычисление определителя разложением по строке(столбцу)
- •5.Обратная матрица и ее вычисление
- •6.Ранг матрицы. Элементарные преобразования матриц
- •7.Системы линейных уравнений. Основные понятия.
- •8.Решение систем линейных уравнений матричным методом
- •9.Формулы Крамера
- •10.Решение систем линейных уравнений методом Гаусса
- •11.Теорема Кронекера-Капелли
- •12.Балансовая модель.
- •13.Векторы. Линейные операции над векторами.
- •14.Разложение вектора на составляющие.
- •15.Деление отрезка в данном отношении.
- •16.Направляющие косинусы и длина вектора. Условие коллинеарности двух векторов
- •17.Скалярное произведение векторов и его свойства. Угол между двумя векторами. Условие ортогональности двух векторов.
- •18.Векторное произведение двух векторов, его свойства и геометрический смысл
- •19.Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •20.Понятие линейного(векторного) пространства.
- •21.Размерность и базис векторного пространства.
- •22.Матрица перехода от одного базиса к другому. Преобразование координат вектора при изменении базиса.
- •23.Евклидово пространство. Ортонормированный базис.
- •24.Линейный оператор и его матрица.
- •25.Собственные значения и собственные векторы линейного оператора.
- •26.Квадратичная форма и ее матрица. Свойства квадратичных форм. Условие знакоопределенности квадратичной формы.
- •27.Линейная модель обмена
- •28.Уравнение линии на плоскости. Различные виды уравнения прямой на плоскости. Приведенное и общее уравнения прямой.
- •29.Угол между прямыми. Критерии перпендикулярности и параллельности двух прямых. Точка пересечения двух прямых. Расстояние от точки до прямой.
- •30.Кривые второго порядка: окружность и эллипс.
- •31.Гипербола и ее каноническое уравнение.
- •32.Парабола и ее каноническое уравнение.
- •33. Уравнение прямой в пространстве(параметрическое и каноническое)
- •34. Уравнение плоскости в пространстве. Расстояние от точки до плоскости.
- •35.Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью
24.Линейный оператор и его матрица.
Если
задан закон (правило). По которому каждому
вектору
пространства
ставится в соответствие единственный
вектор
пространства
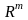 ,
то говорят, что задан оператор
(преобразование, отображение)
,
то говорят, что задан оператор
(преобразование, отображение)
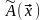 ,
действующий из
в
,
и записывают
,
действующий из
в
,
и записывают
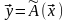 .
При этом вектор
называют образом
вектора
,
а сам вектор
- прообразом
вектора
.
Оператор
.
При этом вектор
называют образом
вектора
,
а сам вектор
- прообразом
вектора
.
Оператор
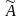 называется линейным,
если для любых векторов
и
пространства
и любого числа
выполняются соотношения:
называется линейным,
если для любых векторов
и
пространства
и любого числа
выполняются соотношения:
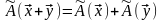 -
свойство аддитивности оператора;
-
свойство аддитивности оператора;
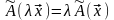 -
свойство однородности оператора.
-
свойство однородности оператора.
Теорема
. Каждому
линейному оператору
-мерного
пространства соответствует матрица
-го
порядка, и наоборот: всякой матрице
-го
порядка соответствует линейный оператор
-мерного
пространства. Связь между вектором
и его образом
можно выразить в матричной форме
уравнением: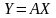 ,
,
де
- матрица линейного оператора,
и
 - матрицы-столбцы из координат векторов
и
.Пример.
Пусть в пространстве
- матрицы-столбцы из координат векторов
и
.Пример.
Пусть в пространстве
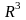 линейный оператор
в базисе
задан матрицей
линейный оператор
в базисе
задан матрицей
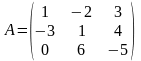 .
Найти образ
вектора
.
Найти образ
вектора
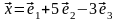 .
.
Решение: По формуле
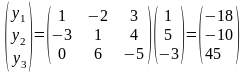
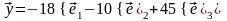
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема
2.
Матрицы
и
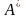 линейного оператора
в базисах
и
связаны соотношением
линейного оператора
в базисах
и
связаны соотношением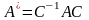 ,
где
,
где
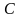 - матрица перехода от старого базиса к
новому.
- матрица перехода от старого базиса к
новому.
Пример
2.
Матрица
линейного оператора
задана в базисе
:
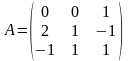 .
Найти ее в базисе
.
Найти ее в базисе
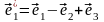 ,
,
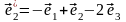 ,
,
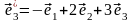 .
.
Решение:
По формуле найдем матрицу перехода от
старого к новому базису:
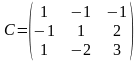 .
.
Найдем.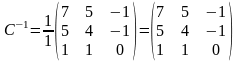 .
.
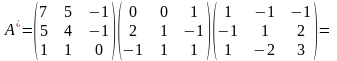
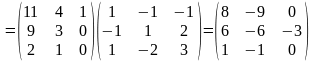
25.Собственные значения и собственные векторы линейного оператора.
Вектор
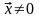 называется собственным
вектором
линейного оператора
,
если найдется такое число
,
что
называется собственным
вектором
линейного оператора
,
если найдется такое число
,
что
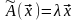 .
Число
называется собственным
значением
оператора
(матрицы
),
соответствующим вектору
.Из
определения следует, что собственный
вектор под действием линейного оператора
переходит в вектор, коллинеарный самому
себе, т.е. умножается на некоторое число.
Равенство можно записать в матричной
форме:
.
Число
называется собственным
значением
оператора
(матрицы
),
соответствующим вектору
.Из
определения следует, что собственный
вектор под действием линейного оператора
переходит в вектор, коллинеарный самому
себе, т.е. умножается на некоторое число.
Равенство можно записать в матричной
форме: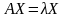 .
.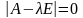 Уравнение
называется характеристическим
уравнением. Определитель
Уравнение
называется характеристическим
уравнением. Определитель
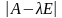 является многочленом
является многочленом
 -ой
степени относительно
.
Этот многочлен называется характеристическим
многочленом
оператора
или матрицы
.
-ой
степени относительно
.
Этот многочлен называется характеристическим
многочленом
оператора
или матрицы
.
Свойства собственных векторов: Собственные векторы, соответствующие различным собственным значениям, линейно независимы.; Если собственные векторы матрицы образуют базис, то в этом базисе матрица оператора имеет диагональный вид, причем ее диагональными элементами являются собственные числа
Для
нахождения собственных значений и
собственных векторов оператора
нужно найти все различные корни
характеристического уравнения
и
для каждого такого корня найти линейно
независимые решения системы уравнений
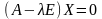 .совокупность
которых образует линейно независимую
систему собственных векторов. Каждому
собственному значению соответствует
хотя бы один собственный вектор, так
как система, определитель которой равен
нулю, имеет хотя бы одно ненулевое
решение.
.совокупность
которых образует линейно независимую
систему собственных векторов. Каждому
собственному значению соответствует
хотя бы один собственный вектор, так
как система, определитель которой равен
нулю, имеет хотя бы одно ненулевое
решение.
Пример
.
Найти собственные значения и собственные
векторы линейного оператора
,
заданного матрицей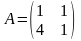 Решение:
Составим характеристическое уравнение
Решение:
Составим характеристическое уравнение
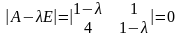 или
или
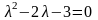 ,
откуда собственные значения линейного
оператора
:
,
откуда собственные значения линейного
оператора
:
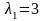 и
и
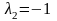 .
.
Находим
собственный вектор
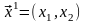 ,
соответствующий собственному значению
,
используя формулу
,
соответствующий собственному значению
,
используя формулу
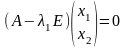 или
или
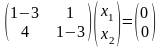 ,откуда
получаем систему:
,откуда
получаем систему: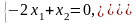 Из
системы имеем
Из
системы имеем
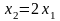 .
Положив
.
Положив
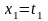 ,
получим, что векторы
,
получим, что векторы
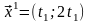 при любом
при любом
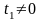 являются собственными векторами
линейного оператора
с собственным значением
.
Аналогично находится собственный вектор
являются собственными векторами
линейного оператора
с собственным значением
.
Аналогично находится собственный вектор
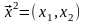 ,
соответствующий собственному значению
:
,
соответствующий собственному значению
:
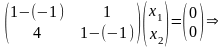
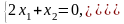
Отсюда
имеем
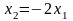 .
Положив
.
Положив
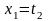 ,
получим, что векторы
,
получим, что векторы
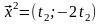 при любом
при любом
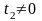 являются собственными векторами
линейного оператора
с собственным значением
.
являются собственными векторами
линейного оператора
с собственным значением
.
