17.Скалярное произведение векторов и его свойства. Угол между двумя векторами. Условие ортогональности двух векторов.

Скалярным произведением векторов и называется число, равное произведению их длин на косинус угла между ними: . Углом между двумя векторами и называется наименьший угол , на который нужно повернуть один из них до совпадения с другим, если эти векторы отложены из одной точки.

Свойства скалярного произведения:

- коммутативность; - ассоциативность; - дистрибутивность; Скалярный квадрат вектора равен квадрату его длины: .

Теорема (критерий перпендикулярности (ортогональности) векторов). Для того, чтобы два вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение равнялось нулю.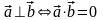 Замечание:

1) .

2) Из формулы следует, что: когда угол между и острый, когда этот угол тупой.

Учитывая формулу и теорему , получаем, что для перпендикулярности двух векторов необходимо и достаточно, чтобы выполнялось равенство: .

.

Пример Дан треугольник с вершинами , , . Найти величину угла .

Решение: ;

Запишем формулу скалярного произведения: .

В координатах: ,

,

Отсюда , , .

18.Векторное произведение двух векторов, его свойства и геометрический смысл

Векторным произведением вектора на вектор называется вектор , такой что:

-вектор перпендикулярен перемножаемым векторам: , ;

- направление вектора определяется по правилу: если смотреть с конца стрелки вектора на плоскость, образованную векторами и , то вращение (внутри плоскости) от к по кратчайшему пути должно происходить против часовой стрелки;

-модуль вектора определяется формулой: ,где - угол между векторами и Свойства векторного произведения.

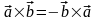- (антикоммутативность).

- (ассоциативность).

- (дистрибутивность).

- Критерий коллинеарности векторов:

Теорема . Для того чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы их векторное произведение равнялось нулю: .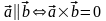

- Векторный квадрат равен нулю: .

- Геометрический смысл векторного произведения. Модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах. Действительно, , что совпадает с формулой площади параллелограмма, известной из курса средней школы.

Найдем произведение:

.

Полученное выражение есть разложение определителя третьего порядка по элементам первой строки, т.е.:

.

19.Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.

Смешанным произведением трех векторов , и называется число, равное , т.е. скалярному произведению векторного произведения первых двух на третий вектор. Найдем выражение для смешанного произведения трех векторов через их координаты, для чего запишем скалярное произведение вектора на вектор

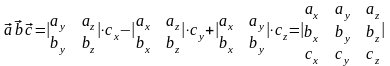
Таким образом, смешанное произведение равно определителю третьего порядка, в строках которого стоят координаты перемножаемых векторов. Смешанное произведение принято обозначать .

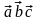Свойства смешанного произведения:

- .

-Геометрический смысл смешанного произведения.

Модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах, как на ребрах Для доказательства этого построим вектор 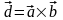, длина которого в соответствии с геометрическим смыслом векторного произведения, равна площади параллелограмма, построенного на векторах и , т.е. площади основания параллелепипеда: . Из определения смешанного произведения , где - угол между векторами и . Когда угол . Для этого случая получим, что высота – объем паралл-да

Условие компланарности векторов Векторы, параллельные одной плоскости, называются компланарными. Очевидно, что два вектора всегда компланарны.

Теорема (критерий компланарности векторов). Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Доказательство: Если три вектора компланарны, можно считать, что они лежат в одной плоскости и тогда объем параллелепипеда, построенного на этих векторах, равен нулю, т.е. смешанное произведение равно нулю. Если наоборот, смешанное произведение равно нулю, то объем параллелепипеда равен нулю и, значит, все векторы параллельны одной плоскости (компланарны) или хотя бы один из них равен нулю, что тоже означает компланарность всех трех векторов. Другими словами, необходимым и достаточным условием компланарности трех векторов является равенство нулю определителя, составленного из координат этих векторов: .

Пример . Найти векторное произведение для векторов , .

.
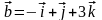
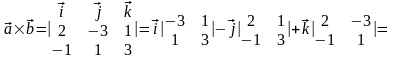