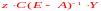- •1.Матрицы, действия над матрицами. Свойства действий.
- •2.Определители второго порядка. Алгебраические дополнения и миноры.
- •3.Определители третьего порядка. Вычисление по правилу треугольника.
- •4.Определитель п-ого порядка, его свойства. Вычисление определителя разложением по строке(столбцу)
- •5.Обратная матрица и ее вычисление
- •6.Ранг матрицы. Элементарные преобразования матриц
- •7.Системы линейных уравнений. Основные понятия.
- •8.Решение систем линейных уравнений матричным методом
- •9.Формулы Крамера
- •10.Решение систем линейных уравнений методом Гаусса
- •11.Теорема Кронекера-Капелли
- •12.Балансовая модель.
- •13.Векторы. Линейные операции над векторами.
- •14.Разложение вектора на составляющие.
- •15.Деление отрезка в данном отношении.
- •16.Направляющие косинусы и длина вектора. Условие коллинеарности двух векторов
- •17.Скалярное произведение векторов и его свойства. Угол между двумя векторами. Условие ортогональности двух векторов.
- •18.Векторное произведение двух векторов, его свойства и геометрический смысл
- •19.Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •20.Понятие линейного(векторного) пространства.
- •21.Размерность и базис векторного пространства.
- •22.Матрица перехода от одного базиса к другому. Преобразование координат вектора при изменении базиса.
- •23.Евклидово пространство. Ортонормированный базис.
- •24.Линейный оператор и его матрица.
- •25.Собственные значения и собственные векторы линейного оператора.
- •26.Квадратичная форма и ее матрица. Свойства квадратичных форм. Условие знакоопределенности квадратичной формы.
- •27.Линейная модель обмена
- •28.Уравнение линии на плоскости. Различные виды уравнения прямой на плоскости. Приведенное и общее уравнения прямой.
- •29.Угол между прямыми. Критерии перпендикулярности и параллельности двух прямых. Точка пересечения двух прямых. Расстояние от точки до прямой.
- •30.Кривые второго порядка: окружность и эллипс.
- •31.Гипербола и ее каноническое уравнение.
- •32.Парабола и ее каноническое уравнение.
- •33. Уравнение прямой в пространстве(параметрическое и каноническое)
- •34. Уравнение плоскости в пространстве. Расстояние от точки до плоскости.
- •35.Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью
9.Формулы Крамера
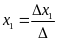 ,
,
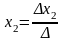 ,
…,
,
…,
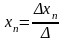 ,где
,где
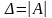 .
.
Формулы называются формулами Крамера .
Пример . Решить систему уравнений по формулам Крамера.
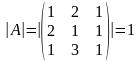
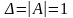 .
.
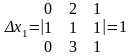 ,
,
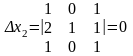 ,
,
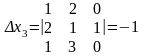 .
.
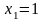 ,
,
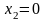 ,
,
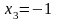
10.Решение систем линейных уравнений методом Гаусса
Метод Гаусса – метод последовательного исключения неизвестных. Этот метод является универсальным потому, что позволяет решать системы любого числа уравнений с любым числом неизвестных, а если система не имеет решения, то метод позволяет установить это в ходе решения. Сущность метода заключается в том, что посредством элементарных преобразований система приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) неизвестных, находятся все остальные неизвестные.
Таким образом, если данная система уравнений после выполнения ряда элементарных преобразований приводится к треугольной системе , то это означает, что система является совместной и определенной. Если же данная система (после элементарных преобразований приводится к ступенчатой системе , то система является совместной и неопределенной.
Переход системы к ступенчатой или треугольной системе называется прямым ходом метода Гаусса, нахождение неизвестных из последних систем – обратным ходом.
Пример . Решить систему уравнений методом Гаусса:
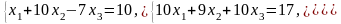
Шаг
1: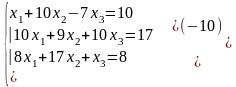
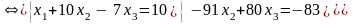
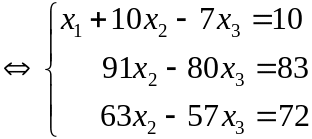
Шаг 2:
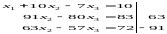
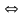
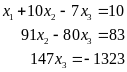
Привели
систему уравнений к
треугольному виду.
Теперь методом обратного
хода
можно определить сначала значение
переменной
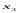 из последнего уравнения системы, затем
значение переменной
из последнего уравнения системы, затем
значение переменной
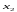 из второго уравнения, и, наконец, значение
переменной
из второго уравнения, и, наконец, значение
переменной
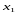 из первого уравнения.
из первого уравнения.


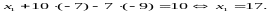
Ответ: (17,-7,-9).
11.Теорема Кронекера-Капелли
Теорема
Кронекера-Капелли (теорема существования
решения системы линейных уравнений).Для
того, чтобы система линейных уравнений
была совместной, необходимо и достаточно
чтобы ранг матрицы системы был равен
рангу ее расширенной матрицы т.е.
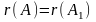 .Для
совместных систем линейных уравнений
верны следующие теоремы:
.Для
совместных систем линейных уравнений
верны следующие теоремы:
Теорема
1. Если
ранг матрицы совместной системы равен
числу неизвестных, т.е.
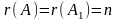 ,
то система уравнений имеет единственное
решение.
,
то система уравнений имеет единственное
решение.
Теорема
2. Если
ранг матрицы совместной системы меньше
числа неизвестных, т.е.
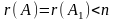 ,
то система уравнений неопределенная
и имеет бесконечное множество решений.
,
то система уравнений неопределенная
и имеет бесконечное множество решений.
Замечание.
Если ранги матрицы системы и расширенной
матрицы не равны (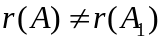 ),
то система уравнений несовместна
(решений нет).
),
то система уравнений несовместна
(решений нет).
12.Балансовая модель.
Рассмотрим
производство, состоящее из взаимосвязанных
подразделений (отраслей), которые в
процессе производства продукции
затрачивают некоторое количество
продукции, производимой в других
подразделениях. Таким образом, валовой
продукт всех подразделений складывается
из двух частей –
конечного продукта и внутрипроизводственного
потребления. Математическая
модель, позволяющая их анализировать,
была разработана в 1936 г. экономистом
В. Леонтьевым.
валовой
продукт = конечный продукт +
внутрипроизводственное потребление
в
матричных обозначениях, в виде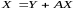 .
Это уравнение называется уравнением
межотраслевого баланса (балансовой
моделью или моделью Леонтьева).
Теперь количество продукции
.
Это уравнение называется уравнением
межотраслевого баланса (балансовой
моделью или моделью Леонтьева).
Теперь количество продукции
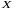 ,
которое необходимо произвести, чтобы
обеспечить заданное количество конечного
продукта
,
которое необходимо произвести, чтобы
обеспечить заданное количество конечного
продукта
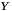 ,
получается как решение матричного
уравнения
,
получается как решение матричного
уравнения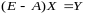
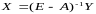 .
.
Матрица
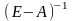 называется матрицей
коэффициентов полных производственных
затрат.
Разница между полными производственными
затратами и прямыми производственными
затратами называется косвенными
затратами. Таким образом, матрица
называется матрицей
коэффициентов полных производственных
затрат.
Разница между полными производственными
затратами и прямыми производственными
затратами называется косвенными
затратами. Таким образом, матрица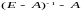 есть
матрица
коэффициентов косвенных производственных
затрат.
есть
матрица
коэффициентов косвенных производственных
затрат.
Чистый
продукт
отрасли есть ее валовой продукт минус
то количество продукции, которое было
затрачено на производство этого валового
продукта во всех отраслях/ Определим
затраты сырья в
пересчете на 1 единицу конечной продукции
 –й
отрасли. С учетом соотношения
–й
отрасли. С учетом соотношения
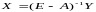 получаем
получаем
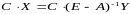 .
.
Таким
образом, матрица
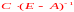 есть
матрица коэффициентов полных затрат
сырья. Если известен вектор цен за одну
единицу сырья каждого вида
есть
матрица коэффициентов полных затрат
сырья. Если известен вектор цен за одну
единицу сырья каждого вида
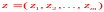 то
полные затраты на производство конечного
продукта
то
полные затраты на производство конечного
продукта
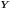 равны
равны