
- •1.Матрицы, действия над матрицами. Свойства действий.
- •2.Определители второго порядка. Алгебраические дополнения и миноры.
- •3.Определители третьего порядка. Вычисление по правилу треугольника.
- •4.Определитель п-ого порядка, его свойства. Вычисление определителя разложением по строке(столбцу)
- •5.Обратная матрица и ее вычисление
- •6.Ранг матрицы. Элементарные преобразования матриц
- •7.Системы линейных уравнений. Основные понятия.
- •8.Решение систем линейных уравнений матричным методом
- •9.Формулы Крамера
- •10.Решение систем линейных уравнений методом Гаусса
- •11.Теорема Кронекера-Капелли
- •12.Балансовая модель.
- •13.Векторы. Линейные операции над векторами.
- •14.Разложение вектора на составляющие.
- •15.Деление отрезка в данном отношении.
- •16.Направляющие косинусы и длина вектора. Условие коллинеарности двух векторов
- •17.Скалярное произведение векторов и его свойства. Угол между двумя векторами. Условие ортогональности двух векторов.
- •18.Векторное произведение двух векторов, его свойства и геометрический смысл
- •19.Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
- •20.Понятие линейного(векторного) пространства.
- •21.Размерность и базис векторного пространства.
- •22.Матрица перехода от одного базиса к другому. Преобразование координат вектора при изменении базиса.
- •23.Евклидово пространство. Ортонормированный базис.
- •24.Линейный оператор и его матрица.
- •25.Собственные значения и собственные векторы линейного оператора.
- •26.Квадратичная форма и ее матрица. Свойства квадратичных форм. Условие знакоопределенности квадратичной формы.
- •27.Линейная модель обмена
- •28.Уравнение линии на плоскости. Различные виды уравнения прямой на плоскости. Приведенное и общее уравнения прямой.
- •29.Угол между прямыми. Критерии перпендикулярности и параллельности двух прямых. Точка пересечения двух прямых. Расстояние от точки до прямой.
- •30.Кривые второго порядка: окружность и эллипс.
- •31.Гипербола и ее каноническое уравнение.
- •32.Парабола и ее каноническое уравнение.
- •33. Уравнение прямой в пространстве(параметрическое и каноническое)
- •34. Уравнение плоскости в пространстве. Расстояние от точки до плоскости.
- •35.Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью
1.Матрицы, действия над матрицами. Свойства действий.
Прямоугольная
таблица составленная из
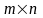 чисел
чисел
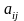 ,
называется матрицей
размером
Числа
называются элементами
матрицы.
Горизонтальный ряд чисел называется
строкой,
а вертикальный – столбцом
матрицы.
Первый индекс
,
называется матрицей
размером
Числа
называются элементами
матрицы.
Горизонтальный ряд чисел называется
строкой,
а вертикальный – столбцом
матрицы.
Первый индекс
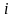 – номер строки, второй
– номер строки, второй
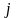 – номер столбца .Матрицу принято
обозначать заглавными буквами: A,
B.
Матрица, в которой число строк не равно
числу столбцов (
– номер столбца .Матрицу принято
обозначать заглавными буквами: A,
B.
Матрица, в которой число строк не равно
числу столбцов ( ),
называется прямоугольной
Матрица,
в которой число строк равно числу
столбцов, называется квадратной.
Причем число ее строк или столбцов
называется порядком
матрицы.
Последовательность
элементов квадратной матрицы с одинаковыми
индексами (
),
называется прямоугольной
Матрица,
в которой число строк равно числу
столбцов, называется квадратной.
Причем число ее строк или столбцов
называется порядком
матрицы.
Последовательность
элементов квадратной матрицы с одинаковыми
индексами (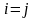 )
называется главной
диагональю
матрицы.
Если
в квадратной матрице все недиагональные
элементы равны нулю , то матрица называется
диагональной.
Квадратная
диагональная матрица, у которой элементы
главной диагонали равны единице,
называется единичной
матрицей E. Матрица,
все элементы которой равны нулю,
называется нуль-матрицей.
Матрица,
состоящая только из одной строки,
называется матрицей-строкой.
Матрица,
состоящая только из одного столбца,
называется матрицей-столбцом.
Матрица
)
называется главной
диагональю
матрицы.
Если
в квадратной матрице все недиагональные
элементы равны нулю , то матрица называется
диагональной.
Квадратная
диагональная матрица, у которой элементы
главной диагонали равны единице,
называется единичной
матрицей E. Матрица,
все элементы которой равны нулю,
называется нуль-матрицей.
Матрица,
состоящая только из одной строки,
называется матрицей-строкой.
Матрица,
состоящая только из одного столбца,
называется матрицей-столбцом.
Матрица
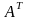 называется транспонированной
по отношению к матрице A,
если она получена из матрицы A
заменой строк этой матрицы ее.
называется транспонированной
по отношению к матрице A,
если она получена из матрицы A
заменой строк этой матрицы ее.
Действия над матрицами: - Суммой двух матриц A и B одинакового размера ( ) называется матрица C того же размера, элементы которой равны сумме соответствующих элементов матриц A и B.Свойства сложения матриц:
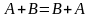 – коммутативность;
– коммутативность;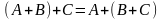 – ассоциативность.
– ассоциативность.
-
Произведением
матрицы A
на матрицу B
называется матрица C=A*B.Матрицы
A
и B,
для которых
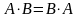 ,
называются коммутативными.
Произведение
двух не нулевых матриц может оказаться
равным нуль-матрице. Получается матрица,
содержащая столько строк, сколько их
имеет первая матрица, и столько столбцов,
сколько их имеет вторая матрица Свойства
умножения матриц:
,
называются коммутативными.
Произведение
двух не нулевых матриц может оказаться
равным нуль-матрице. Получается матрица,
содержащая столько строк, сколько их
имеет первая матрица, и столько столбцов,
сколько их имеет вторая матрица Свойства
умножения матриц:
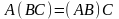 – ассоциативность;
– ассоциативность;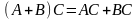 – дистрибутивность.
– дистрибутивность.
2.Определители второго порядка. Алгебраические дополнения и миноры.
Определителем
(или детерминантом)
второго порядка, называется число,
определяемое по формуле: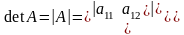 .
.
Понятие определителя только для квадратных матриц
Числа
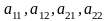 называются элементами
определителя.
называются элементами
определителя.
Минором элемента матрицы А, называется определитель матрицы, полученной из исходной вычеркиванием -ой строки и -ого столбца.
Алгебраическим
дополнением
элемента матрицы называется его минор,
взятый со знаком плюс, если сумма номеров
строки и столбца, в которых стоит этот
элемент, четна, и со знаком минус, если
эта сумма нечетна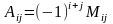 .
.
3.Определители третьего порядка. Вычисление по правилу треугольника.
Определителем (или детерминантом) n-го порядка, называют число, получаемое из элементов матрицы по определенному закону – закону раскрытия определителя. Метод треугольника:





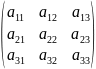 =
=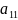 *
*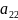 *
* +
+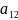 *
*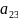 *
*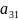 +
+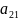 *
*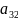 *
*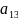 -
*
*
-
*
*
-
*
*
-
*
*
-
*
*
-
*
*
4.Определитель п-ого порядка, его свойства. Вычисление определителя разложением по строке(столбцу)
Определителем (или детерминантом) n-го порядка, называют число, получаемое из элементов матрицы по определенному закону – закону раскрытия определителя:
Определитель n-го порядка равен сумме попарных произведений элементов какой либо его строки (или столбца) на их алгебраические дополнения. Таким образом, любой определитель n-го порядка сводится к сумме n определителей n-1-го порядка. Вычислить определитель третьего порядка:
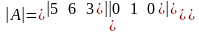 .
.
Решение:
раскроем определитель по элементам
второй строки: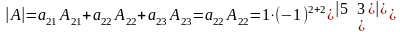 .
.
Свойства определителей:
-Если все элементы какой-либо строки (или столбца) матрицы равны нулю, то определитель равен нулю.
-Если
все элементы какой-либо строки (или
столбца) матрицы умножить на число
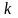 ,
то ее определитель умножится на это
число
.
,
то ее определитель умножится на это
число
.
-Определитель
не изменится, если его строки поменять
местами с соответствующими столбцами,
т.е.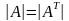
-При перестановке двух строк (или столбцов) матрицы ее определитель изменит знак на противоположный.
-Определитель с двумя одинаковыми строками (или столбцами) равен нулю.
-Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю.
-Если к элементам какой-либо строки (или столбца) матрицы прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменится.
