71. Проводники в электрическом поле. Условие равновесия зарядов на проводнике. Электроемкость уединенного проводника. Единица электроемкости.

Проводник-вещ-ва, которые содержат эл.заряды способные перемещаться под действием как угодно малой силы. Бывают: твердые, жидкие, газообразные.

Металл имеет кристаллическую структуру, в узлах кристаллической решетки которой находятся в положении заряженных ионы. Эти ионы представляют собой атомы металлов в которых отсутствует 1 или 2 валентных электронов( в зависимости от природы метала) . Валентные электроны отщепившиеся от атомов заполняют пространства кристаллической решетки в виде электронного газа. Эти валентные электроны явл. электронами проводимости, т.е. способны перемещаться под действием как угодно малой силы. Любому проводнику можно сообщить заряд. Но проводнику можно сообщить избыточный эл. Заряд и заряд сообщенный распределенный по поверхности проводника так, как диктует условие равновесия. Если взять уединенный проводник и сообщить ему некоторый дополнительный эл. Заряд, это выполненная работа, то тот заряд будет отталкиваться. Чем больше заряд проводника, тем больше его потенциал.

q=c*

Заряд, который находится в проводнике q и его потенциал , связаны линейной зависимостью.

Коэффициент пропорциональности между зарядом уединенного проводника

q и потенциалом называется электроемкостью проводника.

Электроемкость зависит от:

-размера проводника

-формы

-диэлектрических свойств среды, в которой находится проводник.

Ед. электроемкости =Ф(фарад) Ф = Кл/В

Фарад - электроемкость такого уединенного проводник, потенциал которого изменяется на 1 В при сообщении заряда проводника 1 Кл.

72. Конденсаторы. Расчет емкости плоского конденсатора.

Конденсатор- устройство предназначенное для накопления эл.заряда. Конд-р предст.собой 2а проводника, находящихся на малом расст. Друг от др. р, разделенные слоем диэлектрика. Проводники, образующие конд-р называются его обкладками. По форме обкладок различ: плоские цилиндрические и сферические конд-ры. Основной характеристикой конденсатора является его ёмкость С. С- коэффициент пропорциональности между зарядом и разностью потенциалов между его обкладками. Емкость плоского конденсатора зависит от площади пластин, расстояния между ними и материала (диэлектрика), заполняющего пространство между пластинами. где С - емкость Q - накопленная энергия U - напруга на обкладках.

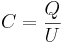
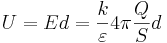
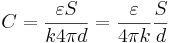
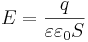
75.Постоянный ток. Его характеристики и условия существования.

Эл.ток – это упорядочное движение заряженных частиц или макроскопических заряженных тел. Различают токи: конвекционные, проводимости. Конвекц. токи – это упорядочное движение макроскопических заряженных тел. Токи проводимости – это упоряд. движение заряженных частиц в вакууме или в веществе. Токи проводимости возникают под действием электрического поля. Условия существования тока проводимости:1) наличие свободных электрических зарядов;2) наличие электрического поля перем. к заряду. Количественной характеристикой электрического поля является сила тока ( I ) .Сила тока ( I ) – скалярная величина и равна отношению зарядов dq переносимого током через некоторую поверхность s за малый промежуток времени dt к длительности этого промежутка времени. I=dq/dt (1) Если сила тока во времени не меняется , то ток называется постоянным. I=const I(const)= q/t (2) .Для характеристики электрического тока вводится понятие плотность. J(вектор) – численно равен отношению силы тока dI через поверхность ds перпендикулярную к напр. Тока к величине площади этой поверхности. J(вектор)= dI/ds (3) J(вектор)- вектор плотности тока. ед. I=A (ампер) .ед. плотности тока J= A/m (квадратный) .Вектор плотности тока для тока проводимости J можно выразить через носитель тока , сих заряд, скорость движения. J(вектор) = nq +v(вектор) (4)

Основные положения этой теории сводятся к следующим:

1). Носителями тока в металлах являются электроны, движение которых подчиняется законом классической механики.

2). Поведение электронов подобно поведению молекул идеального газа (электронный газ).

3). При движении электронов в кристаллической решетке можно не учитывать столкновения электронов друг с другом.

4). При упругом столкновении электронов с ионами электроны полностью передают им накопленную в электрическом поле энергию.

Средняя тепловая скорость хаотического движения электронов приТ≈300К составляет  .

При включении электрического поля на хаотическое движение электронов накладывается упорядоченное движение (называемое иногда«дрейфовым»), происходящее с некоторой средней скоростью  ; возникает направленное движение электронов – электрический ток. Плотность тока определяется по формуле .

Оценки показывают, что при максимально допустимой плотности тока в металлах j = 10⁷ А/м² и концентрации носителей 10²⁸ – 10²⁹м^-3 ,  . Таким образом, даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов  .

.Вывод закона Ома по электронной теории.

Пусть в металлическом проводнике существует электрическое по­ле напряженностью Е=const. Co стороны поля заряд еиспытывает действие силы F=eE и приобретает ускорение а=F/m=еЕ/т. Таким образом, во время сво­бодного пробега электроны движутся рав­ноускоренно, приобретая к концу свобод­ного пробега скорость

v_max= еE<t>.

где <t>—среднее время между двумя последовательными соударениями элек­трона с ионами решетки.

Согласно теории Друде, в конце сво­бодного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упо­рядоченного движения становится равной нулю. Следовательно, средняя скорость направленного движения электрона

<v>=(v_max+0)/2=eE<t>/(2m). (1)

Классическая теория металлов не учи­тывает распределения электронов по ско­ростям, поэтому среднее время <t> сво­бодного пробега определяется средней длиной свободного пробега <l> и средней скоростью движения электронов относи­тельно кристаллической решетки провод­ника, равной <u>+(v) (<u>—средняя скорость теплового движения электронов), было показано, что (v)<< <u>, поэтому

<t>=<l>/<u>.

Подставив значение <t> в формулу (1), получим

<v>=eE<l>/(2m<u>).

Плотность тока в металлическом провод­нике, по (96.1),

откуда видно, что плотность тока пропор­циональна напряженности поля,

т. е. получили закон Ома в дифференци­альной форме (ср. с (98.4)). Коэффициент пропорциональности между j и Е есть не что иное, как удельная проводимость ма­териала

которая тем больше, чем больше концен­трация свободных электронов и средняя длина их свободного пробега.

Произведенные Лоренцем, уточненные расчеты с учетом классического распределения по скоростям привели к замене в теоретической формуле множителя 3 на 2 и к резкому увеличению расхождения теории с опытом. Второе затруднение классической электронной теории возникло при сопоставлении с опытом формул для теплоемкостей. Согласно электронной теории теплоемкость единицы объема электронного газа равна   , где n - концентрация свободных электронов.

Третьим затруднением классической электронной теории металлов явилась невозможность правильно объяснить с ее помощью температурную зависимость сопротивления. Опыт показывает, что сопротивление металлических проводников линейно возрастает с температурой по закону