61. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона.

Электр. заряд – это свойство элементарных частиц.

В природе существует только два типа электрических зарядов: положительные и отрицательные.

Опытным путем (1910-1914) американский физик Р.Милликен показал, что электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда e=1.6*10^-19 Кл. Электрон(m_e=9.11*10^-31 кг) и протон(m_p=1.67*10^-27 кг) являются соответственно носителями элементарных отрицательных и положительных зарядов.

Электрический заряд измеряется в Кулонах(Кл) – электр. заряд, проходящий через поперечное сечение проводника при силе 1 А за время 1 с. (Кл=6,25*10¹⁸*e).

Одноименные электр. заряды отталкиваются, разноименные – притягиваются.

Закон сохранения зарядов: алгебраическая сумма электрических зарядов любой замкнутой системы(система, не обменивающаяся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы.(установлен в 1834 г. англ. физиком М.Фарадеем).

В зависимости от концентрации свободных зарядов тела делятся на проводники(первого и второго рода), полупроводники и диэлектрики.

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам q₁ и q₂ и обратно пропорциональна квадрату расстояния r между ними:

F=k .

Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.

Сила F направлена по прямой, соединяющей взаимодействующие заряды, т.е. является центральной, и соответствует притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов. Эта сила называется кулоновской силой.

62. Электрическое поле. Напряженность электрического поля. Единицы напряженности электрического поля.

Электрич. поля подчин. принц. суперпозиций. Если электрич. поле созд. не отдельн. электр. зарядом, а сист., состоящ. из n-малое электрич. зарядов, то результир. напряж-ть Е электр. поля явл. векторн. суммой напряж-тей электр. полей, созд. кажд. зар-ом по отдел-ти, т.е.: 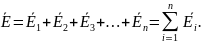(ед. =Н/Кл.) Потенциал результир. поля наход. как алгебр. сумма потенц. энергетич. полей электр. поля, т.е.: (ед. В(Вольт)=Дж/Кл). Электрич. диполь – это сист., сост. из 2-ух точечн. разноим. электрич. зар-ов, равн. по вел-не, находящ. на малом расстоян. друг от друга. Электрич. диполь. мом-т: 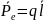, где - электрич. заряд(ед. =Кл(Кулон)), – в-р, численно равн. расстоян. между зар-ами и направлен. от отрицат. заряда к положит; ед. 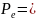Кл×м. Напряж-ть электр. поля в люб. точ. 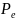диполя: , где - электрич. диполь. мом-т, 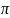= 3,14, - электрическая постоянная( ), - относит. диэлектрич. проницае-ть среды(безразмерная величина), 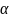- угол между и направлением на точку наблюдения , r — расстояние от точки А до середины плеча диполя. Потенциал электр. поля в люб. точ. диполя: .