
- •15. Кинематика вращательного движения. Угловая скорость и угловое ускорение. Связь между линейной и угловой скоростью.
- •16.Связь угловой скорости и углового ускорения с линейным полным, тангенциальным и нормальным ускорениями.
- •Вопрос 19. Основной закон динамики вращательного движения для системы материальных точек и для тела, шарнирно закрепленного в одной точке .(уравнение моментов)
- •Вопрос 20. Момент импульса твердого тела относительно неподвижной оси. Основной закон динамики вращательного движения для тела, вращающегося относительно неподвижной оси.
- •24. Работа постоянной и переменной силы. Мощность. Единицы работы и мощности.
- •27. Кинетическая энергия механической системы при поступательном движении
- •28. Кинетическая энергия вращательного движения
- •29. Полная механическая энергия. Консервативные системы. Закон сохранения полной механической энергии.
- •31. Классическая теорема сложения скоростей. Мех. Принцип относительности.
- •35. Пространственно-временной интервал
- •36. Релятивистский з-н сложения скоростей.
- •61. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона.
- •62. Электрическое поле. Напряженность электрического поля. Единицы напряженности электрического поля.
- •63. Потенциал электростатического поля. Единицы потенциала.
- •65. Принцип суперпозиции электростатических полей. Расчет электрического поля диполя методом супер позиции.
- •66. Поток вектора напряженности электрического поля. Теорема Остроградского-Гаусса для электрического поля в вакууме.
- •67. Расчет поля, создаваемого бесконечной плоскостью, равномерно заряженной по поверхности
- •70.Расчет напряженности электрического поля в диэлектрике.Относительная диэлектрическая проницаемость вещества.Вектор механического смещения.
- •71. Проводники в электрическом поле. Условие равновесия зарядов на проводнике. Электроемкость уединенного проводника. Единица электроемкости.
- •72. Конденсаторы. Расчет емкости плоского конденсатора.
- •75.Постоянный ток. Его характеристики и условия существования.
Вопрос №5
Первый закон Ньютона. Инерциальные системы отсчета
Основы классической динамики составляют 3 закона и 3 закона сохранения:
-импульса
-момента импульса
-полной механической энергии
Эти законы являются аксиомами (постулаты).
1-й закон Ньютона:
Любая материальная точка движется равномерно и прямолинейно или сохраняет состояние покоя до тех пор пока воздействие со стороны других тел (мат. точек) не изменит это состояние.
Этот закон также называют законом инерции.
1-й закон Ньютона выполняется не любой СО.
Системы отсчета ,в которых выполняется 1-й закон Ньютона называются инерциальными .
Способность тел двигаться или сохранять состояние покоя ,при отсутствии воздействия других те называется инерцией.
Все тела обладают инертностью.
В природе существуют инерциальные системы отсчета.
Вопрос №6 Масса, импульс, сила. Второй закон Ньютона для материальной точки. Единицы силы, массы и импульса.
Для количественного описания динамики движения вводятся понятия массы, импульса и силы.
Масса – количественная мера инертности тела. Это есть скалярная величина. Так же масса – величина аддетивная (суммируемая ) ,т.е. масса тела (системы) равна сумме масс отдельных ее частей m= m1+m2+…mn.
[m]= M; едm=кг
Импульс мат. точки – векторная величина, численно равная произведению массы мат. точки m на ее скорость v. Импульс суммируемая величина. Также импульс называют количеством движения.
p= mv
едp= (кг* м)/c
[p]=([m]*[l])/[t]=(M*L)/T=MLT-1
Сила – количественная мера воздействия одного тела на другое. Это векторная величина.
Если на одно тело действует несколько сил, то их действие можно заменить одной силой F , которая является суммой (векторной) всех сил, действующих на тело.
F=F1+F2+F3+…+Fn= ∑Fi
Сила F называется результирующей. В отдельных случаях можно указать точку приложения силы. Единица силы вводится из 2-го закона Ньютона для мат. точки.
Второй закон Ньютона для мат. точки.
1)Скорость изменения импульса мат. точки по времени равно результирующей силе, действующей на эту точку:
dP/dt=F
d(mv)/dt=F
Если m=const, то mdv/dt=ma=F
7.Третий закон Ньютона. Границы применимости законов Ньютона.
3-ий закон Ньютона: действие одного тела на другое всегда имеет характер взаимодействия. Две мат.точки действуют друг на друга с силами равными по величине, но противоположными по знаку.
механика Ньютона неприменима, если относительные скорости точек сравнимы со скоростью света [это область релятивистской или эйнштейновской механики]; неприменима механика классическая и к изучению явлений микромира [это область квантовой механики]. Но они основаны на классической механики. В остальных областях => классическая механика даёт достаточно точные результаты.
8. Масса, импульс и центр масс системы мат.точек и абсолютно твёрдого тела. Второй закон Ньютона для системы мат.точек и абсолютно твёрдого тела.
Сис-ма мат.точек – совокупность мат.точек взаимодействующих между собой.
Центр
масс(центр инерции)- точка С радиус-вектор
которой даётся

Скорость центра масс – производная скорости центра масс по времени.
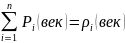 - импульс системы
мат.точек.
- импульс системы
мат.точек.
Импульс системы мат.точек – произведение m массы на скорость её центра масс.
Абсолютно твёрдое тело – тело, расстояние между двумя точками которого всегда остаётся неизменным. Поэтому а.т.т.можно рассматрвиать как совокупность мат.точек жёстко связанных между собой.
Рассмотри систему мат.точек и запишем для каждой точки входящей в систему второй закон Ньютона.

F1 – результатирующая всех внешних сил, действующих на первую точку.
2-ый закон Ньютона для абсолютно твёрдого тела: поступательное движение а.т.т.такое движение при котором любая прямая жёстко связанная с этим телом при движении тела перемещается параллельно самой себе.
При поступательном движении тела все точки тела имеют одинаковые скорости. Поэтому для любой точки тела скорость такая же как и у центра масс.
13.
При соприкосновении движущихся (или приходящих в движение) тел с другими телами, а также с частицами вещества окружающей среды возникают силы, препятствующие такому движению. Эти силы называют силами трения. Действие сил трения всегда сопровождается превращением механической энергии во внутреннюю и вызывает нагревание тел и окружающей их среды.
Существует внешнее и внутреннее трение (иначе называемое вязкостью). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям.
Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении. слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.
Внешнее трение подразделяют на трение покоя (статическое трение) и кинематическое трение. Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения.
В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.
14.
Момент инерции тела относительно некоторой оси z – это сумма произведений масс м. т. Составляющих тело на квадрат их расстояния до оси z.
n
Iz=∑ mizi²
i=1
Момент инерции – это кол. Мера инертности тела при вращательном движении. зависит от массы и от распределения массы по телу.
Собственный момент инерции Ic – это момент инерции тела относ. оси проходящей через его центр масс.
Icк = 2/5 * mR²
Для вычисления мом. инерции тв. Тела исп. Теорема Штейнера
Iz۱=Ic+ma²
Мом. Инерции тв. тела относ. производной оси z۱ = собственному моменту инерции тела Ic + произведение массы тела m на квадрат расстояния a между осью z штрих и z проходящей через центр масс тела параллельно оси z۱
15. Кинематика вращательного движения. Угловая скорость и угловое ускорение. Связь между линейной и угловой скоростью.
Вращение движения тела – движение, при котором все точки тела движутся по окружности, центры которых лежат на одной прямой, назыв. осью вращения.
Траектория движения точки при этом лежит в плоскостях перпендикулярных оси вращения. Ось вращения проходит как внутри тела или быть в ей. Если ось вращения проходит внутри тела, то тела принадл. ось не вращения – неподвижны.
За
равный промежуток времени все точки
вращ.движ. поворачиваются а один и тот
же угол. Для коллич. Оценки вращ.движ.
вводится понятие угловой
скорости.
По определению угловая мгновенная
скорость движения
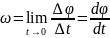 ( 1ая производная поворота ϕ
по времени)
Вектор угловой скорости
направлен вдоль оси вращ. Так, если
смотреть с конца, ω
вращ. Тела происходит против часовой
стрелки. Если угловая скорость постоянна,
движение равномерное.
Время, за
которое тело совершает один полный
поворот, поворачивается на угол 2π,
назыв. период
вращения.
( 1ая производная поворота ϕ
по времени)
Вектор угловой скорости
направлен вдоль оси вращ. Так, если
смотреть с конца, ω
вращ. Тела происходит против часовой
стрелки. Если угловая скорость постоянна,
движение равномерное.
Время, за
которое тело совершает один полный
поворот, поворачивается на угол 2π,
назыв. период
вращения.
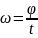
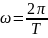
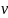 =
=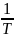 единица измер.
единица измер.
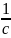 =
= Величина
V
равная
назыв. частотой.
Величина
V
равная
назыв. частотой.
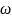 =
=
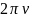 ед.измер
ед.измер
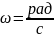
Для
коллич. оценки быстроты изм.угловой
скорости вводится понятие углового
ускорения.
По определению угловое мгновенное
ускорении
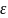 =
=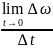 =
=
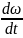
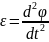 Вектор
так же направле вдоль оси вращения и
совпадает с направлением
,
если тело набирает обороты, противоп.,
если замедляет движение. Ед
Вектор
так же направле вдоль оси вращения и
совпадает с направлением
,
если тело набирает обороты, противоп.,
если замедляет движение. Ед
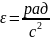 Если
постоянно это будет равномерное вращ.
Движение
Если
постоянно это будет равномерное вращ.
Движение
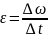
Связь
между линейной и угловой скоростью:
=
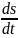 = [
= [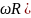
 ^R)
=90
^R)
=90
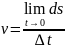 =
=
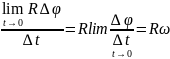
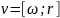
16.Связь угловой скорости и углового ускорения с линейным полным, тангенциальным и нормальным ускорениями.
Линейное
мгновенное ускорение:
а =
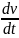 =
=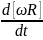 = [
= [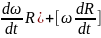 = [
= [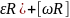
a
=
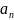 +
+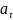
– направлена по касатк траектории движ. - направлена вдоль радиуса к центру окружности

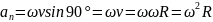
a
=

Вопрос № 17 Момент силы относительно неподвижной точки. Момент силы относительно неподвижной оси.
Момент силы относительно неподвижной точки если есть т. о. и некоторая сила F, то моментом силы F относительно неподвижной т. о. называется вектором M= [r’ ˑ p]
|M| = M ˑ r ˑ Flim (r’,F)
Чтобы определить вектор момента силы, нужно указать плечо силы.
Кратчайшее расстояние оси т. О до линии действия силы называется плечом силы.
d-плечо силы
d=rlimα = rlim (r1 F)
M=dF=rlimαF
Момент силы относительно оси.
Момент силы относительно оси Z-проекция момента силы, взятого относительно некоторой точки на оси Z на эту ось Z.
Единица М = Нˑм
Вопрос № 18 Момент импульса
Момент импульса – динамическая величина.
Импульс – произведение массы материальной точки на её скорость.
P=mU
Момент импульса определяется аналогично моменту силы.
Момент импульса: L = [r1 P]
|L| = L = rˑRlim(r1 R)
Момент импульса относительно неподвижной оси Z – это проекция момента импульса относительно произвольной точки оси на эту ось .
Единица L = мˑНˑс =Нˑмˑс
Единица L = ((кгˑм)/с)ˑм = (кгˑм2)/с
Вопрос 19. Основной закон динамики вращательного движения для системы материальных точек и для тела, шарнирно закрепленного в одной точке .(уравнение моментов)

 =
=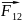 +
+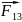 +
+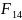 +
+ +
+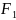
Для 2-ой точки
= +
+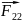 +
+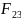 +…+
+…+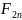 +
+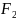 (1)
(1)
Для 3-ей точки

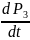 =
=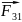 +
+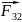 +
+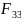 +…+
+…+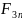 +
+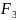
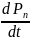 =
=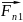 +
+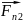 +
+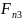 +…+
+…+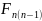 +
+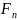
[ ]=[
]=[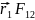 ]+
]+…+[
]+
]+…+[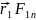 ]+[
]+[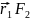 ]
]
[ ]=[
]=[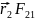 ]+
]+[
]+
]+[ ]+…+[
]+…+[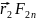 ]+
]
(2)
]+
]
(2)
……………………………………………………………………………
[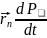 ]=[
]=[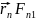 ]+
]+[
]+
]+[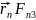 ]+…+[
]+…+[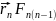 ]+
]
]+
]
[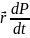 ]=
]=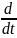 [
[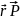 ]
]
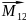 =[
=[ ]
]
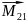 =[
=[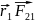 ]
]
 =-
=-
=-
=-
[ ]=
+
]=
+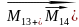 +…+
+…+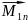 +
+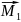
[ ]=
+
]=
+ +
+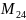 +…+
+…+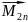 +
+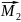 (3)
(3)
………………………………………………………………….
[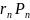 ]=
]=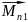 +
+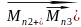 +…+
+…+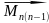 +
+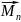

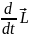 =
+
+…+
=
+
+…+ +
+
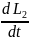 =
+
+…+
+
(4)
=
+
+…+
+
(4)
………………………………………………
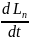 =
+
+…+
+
=
+
+…+
+
Сложим правую и левую часть этих ур-ний
(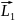 +
+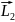 +
+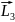 +…+
+…+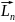 )=
(
+
)+
(
)=
(
+
)+
(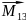 +
+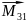 )+
(
)+
(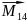 +
+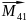 )+…+
(
+
)+…+
+
)+…+
(
+
)+…+
+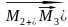 +
+
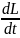 =
=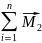 (5)
(5)
=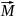 (6)
(6)
=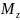 (7)
(7)
Скорость изменения момента импульса(1) для системы матер.точек,взятых относительно неподвижной точки О=результатирующему моменту М всех внешних сил,действующих на эту систему взятой той же точки О.
(6) справедливо также для твёрдого тела шарнирно-закрепленного в одной точке.
