21. Метод резолюций в логике высказываний

Пустой дизъюнкт – дизъюнкт, не содержащий литерала. Обозначим

Пустой дизъюнкт ложен при любых интерпретациях.

Формулы: F = ; F = F

Литералы L и ¬L называют противоположными (контрарными).

Правело резолюции в логике высказываний

Из дизъюнктов X F и ¬X G выводим дизъюнкт F G.

Пример: из дизъюнктов ¬X Y Z и X ¬Y выводим дизъюнкт Y Z ¬Y

Вывод из множества дизъюнктов

Пусть S - множество дизъюнктов.

Выводом из S называется последовательность дизъюнктов D1,D2,..Dn, такая, что каждым дизъюнкт этой последовательности принадлежит S или следует из предыдущего по правилу резолюции.

Дизъюнкт D выводим из S, если существует вывод из S, последним дизъюнктом которого является D.

Пример Если S={¬X Y Z, ¬Y U, X}

D1= ¬X Y Z

D2=¬Y U

D3=¬X Z U – из D1 и D2 по правилу резолюции.

D4=X

D5=Z U – из D3 и D4 по правилу резолюции.

D5 - вывод из S; дизъюнкт Z U выводим из S.

Теорема о полноте метода резолюций

Множество дизъюнктов в логике высказываний S невыполнимо тогда и только тогда, когда из S выводим пустой дизъюнкт.

Доказать с помощью метода резолюций, что формула G является логическим следствием множества формул F1,…, Fk

1. Составляем множество формул T={F1,…, Fk,¬G}.

2. Каждую из этих формул приводим к КНФ и в полученных формулах зачеркиваются знаки конъюнкции (). Получается множество дизъюнктов S.

3. Имеется вывод пустого дизъюнкта из S . Если пустой дизъюнкт выводим из S, то формула G является логическим следствием формул F1,…, Fk. Если из S нельзя вывести пустой дизъюнкт, то G не является логическим следствием формул F1,…,Fk.

Пример: доказать что формула G=Z является логическим следствием формул

F1=¬X Y →X Z; F2=¬Y→Z

1: T={F1,F2,¬G}

2: F1 равносильна X (¬Y Z)

F2 равносильна (Y Z)

Тогда множество дизъюнктов S={X, ¬Y Z, Y Z, ¬Z}

3: ¬Y Z, ¬Z, ¬Y, Y Z, Y, (из множества S выводим пустой дизъюнкт)

Следовательно формула G является логическим следствием формул F1 и F2.

Пример: доказать истинность заключения

(A→B) (C→D); (DB → M); ¬M

(¬A ¬C)

Посылки (в КНФ)

F1=(A→B) (C→D)=(¬A B) (¬C D)

F2=(D B→M)=¬(D B) M=(¬D ¬B M)

F3=¬M

Отрицание заключения в КНФ: ¬G=¬(¬A ¬C)=AC

Множество дизъюнктов

S={A;C;¬M;(¬A B);(¬C D);(¬D ¬B M}

Вывод (резольвенты)

D1=A (¬A B)=B

D2=B (¬D ¬B M)=(¬D M)

D3=(¬D M) (¬C D)=(¬C M)

D4=(¬C M) ¬M=¬C

D5=¬C C=

Истинность значения (¬A ¬C) доказана.

Иллюстрированный вывод в виде графа

Д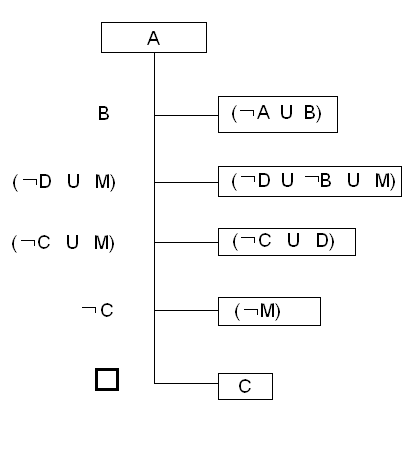 ля иллюстрированного вывода удобно использовать граф типа «дерево», корнем которого является один из дизъюнктов отрицания заключения, а концевыми вершинами ветвей - оставшиеся дизъюнкты отрицания заключения и всех посылок. Узлами графа типа «дерево» являются резольвенты.

«+»: При применении истинности заключения применяют только одно правило: поиск и удаление противоположных (контрарных) литералов на множестве дизъюнктов.

22. Предикаты и операции над ними

Исчисление предикатов – исчисление, в котором наряду с формулами исчисления высказываний используется формулы, в которые могут входить отношения (предикаты), связывающие между собой группы элементов исчисления и кванторы общности и существования.

Исчисления предикатов, в которых под знаком квантора не могут находится символы предикатов называется исчисление предикатов 1 порядка.

Предикат (высказывательная функция) - логическое сказуемое.

Предикат – специальный знак, отражающий определенное отношение между конечным множеством сущностей-аргументов.

Пусть М - непустое множество (предметное множество).

Тогда n-местным предикатом, заданным на М, называется выражение, содержащее n переменных и образующееся в высказывание при замене этих переменных элементами множества М.

Пример: Пусть М есть множество натуральных чисел N, тогда выражения «Х-простое число», «X-четное число», «Х-больше 10» являются одноместными предикатами.

При подстановке вместо X натуральных чисел получаются высказывания «2-простое число», «5 больше 10» и так далее.

Выражение «x больше y» , «x +y=10» является двухместным предикатом.

Выражение «x лежит между y и z» является трехместным предикатом.

Высказывание - нульместный предикат, или предикат, в котором нет переменных для замены.

Предикат с заменяемыми переменными x1,..,xn будет обычно указываться заглавной буквой латинской буквой, после которой в скобках указываются эти переменные.

Пример: P(x1, x2)

Среди переменных в скобках могут быть и фиктивные

Пример: На множестве имен индивидов, университета и специальностей заданы высказывательные функции (предикаты).

Р1(Х)= «х-студент».

Р2(Х,БГТУ)= «студент х университета БГТУ».

Р3(x,y,САПР)= «студент х университета y обучается по специальности САПР».

X,Y- предметные переменные.

БГТУ и САПР – постоянные

На совокупности всех предикатов, заданных на множестве М, вводятся операции конъюнкции, дизъюнкции, отрицания, импликации, эквиваленции.

В логике предикатов I порядка вводится 2 новые операции:

- квантор общности ;

- квантор существования ( ).

Предикат W(x1,..,xn) называется конъюнкцией предикатов U(x1,..,xn) и V(x1,..,xn), заданных на множестве М, если для любых a1,..,an из М высказываний W(a1,..,an) есть конъюнкция высказываний U(a1,..,an) и V(a1,..,an).

Пример: «Существует х такой, что x+y=10» На множестве натуральных чисел это предположение определяется одноместным предикатом P(y). Так Р(2) и Р(9) истинные высказывания, Р(11) ложное.

Если обозначить «x+y=10» через S(x,y) то Р(y) «существует x такой, что S(x,y)». Предикат Р(у) получаем из S(x,y) навешиванием квантора существования на x и пишут P(Y)=( x) S(x,y).

Пусть P(x1,…,xn) – предикаты, заданные на множестве М, у переменная.

Тогда:

-выражение «для каждого у выполняется Р(х1,…,xn)» - предикат, полученный из Р навешиванием квантора общности на переменную у.

-выражение «существует у такой, что выполняется Р(х1,…,xn)» - предикат полученный из Р навешиванием квантора существования на переменную y.

Высказывание xP(x) означает, что область истинности предиката P(x) совпадает с областью значение переменой х. Высказывание ( x)Р(х) означает, что область истинности предиката Р(х) не пустая.