Аналитическое решение.

Интенсивность поломки n-1 оборудования равна

- интенсивность обслуживания

Составим систему уравнений:

Приравняем правые части к нулю:

Решим систему уравнений:

1. Вероятность того, что в системе находятся 1 и более заявки:

2. Среднее число заявок в системе:

3. Среднее число заявок в очереди:

4. Среднее время пребывания заявки в системе

5. Среднее время ожидания в очереди:

6. Среднее время обслуживания:

Задача

10 рыболовных траулеров обслуживаются плавучей базой. Среднее время плавания равно 3 суткам. На базе имеется 1 причал. Среднее время обслуживания 8 часов. Определить среднюю длину очереди; среднее время простоя траулера.

Группа из 10 рыболовных траулеров обслуживается одной плавучей базой. Среднее время плавания траулера равно 3 суткам. На базе имеется один причал. Среднее время обслуживания траулера – 8 часов. Определить:

- среднюю длину очереди;

- среднее время простоя траулера;

- среднее время ожидания заявки в очереди.

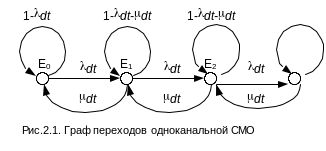
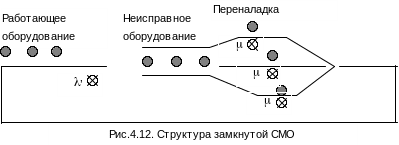
1. Условная схема смо

2. Граф переходов

1. Вероятность того, что в системе находится 1 и более заявок

2. Среднее число заявок в системе

3. Среднее число заявок в очереди

4. Среднее время пребывания заявки в системе

5. Среднее время ожидания в очереди

6. Среднее время обслуживания

Задача

На автозаправочную станцию поступает поток автомашин (пуассоновский) с интенсивностью l=2 авто/мин. Колонка обслуживает машину в среднем за 1,25 мин. Количество работающих колонок равно 5. Длина очереди не превышает количество колонок. Определить: среднее число машин в очереди ; среднее время ожидания в очереди ; вероятность отказа в обслуживании.

Решение.

Это задача о многоканальной Системе Массового Обслуживания с ожиданием.

Введем обозначения

λ = 2 - интенсивность входного потока

t_об = 1.25 - время обслуживания одной колонкой

одного автомобиля

μ = 1 / t_об - среднее число заявок обслуживаемых уз-

лом за единицу времени

S =5 - количество колонок

Рассмотрим вероятности переходов при изменении состояний системы.

Изменение состояния:	Вероятность перехода:
-> -> ->

Вычислим μ :

μ = 1 / t_об μ = 1 / 1.25 =0.8

P_n=λ*P_n-1-( λ+n*µ)*P_n+(n+1)*µ*P_n+1

P₁(t+dt)=λ*P₀(t)-( λ+n*µ)*P₁(t)+(n+1)*µ*P₂(t)

P₂(t+dt)=λ*P₁(t)- ( λ+n*µ)*P₂(t)+(n+1)*µ*P₃(t)

P₃(t+dt)=λ*P₂(t) -( λ+n*µ)*P₃(t)+(n+1)*µ*P₄(t)

P₄(t+dt)=λ*P₃(t) -( λ+n*µ)*P₄(t)+(n+1)*µ*P₅(t)

P₅(t+dt)=λ*P₄(t)-( λ+n*µ)*P₅(t)+S*µ*P₂

P₅(t) = λ*P₄(t)-2*µ*P₅(t)

(4* λ+µ)*P₁=5* λ*P₀+2*µ*P₂

(3* λ+2*µ)*P₂=4* λ*P₁+2*µ*P₃

(2* λ+2*µ)*P₃=3* λ*P₂+2*µ*P₄

( λ+2*µ)*P₄=5* 2*P₃+2*µ*P₅

2*µ*P₅= λ*P₄

P₁=2.5/1*P₀=2.5* P₀

P₂=6.25/2*P₀=3.12* P₀

P₃=15.63/6*P₀=2.6* P₀

P₄=39.06/24*P₀=1.63* P₀

P₅=97.66/120*P₀=0.81* P₀

P₀=1/(1+2.5+3.12+2.6+1.63+0.81)=0.09

1) Найдем среднее число машин в очереди по формуле,

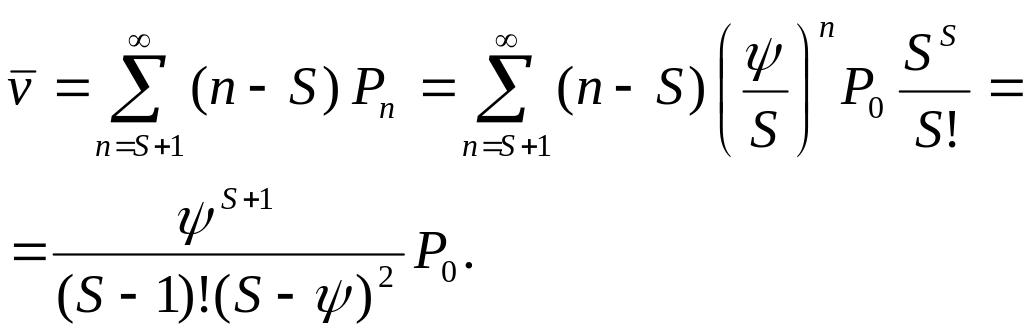
где в свою очередь P₀ есть вероятность простоя узлов обслуживания СМО, когда нет заявок, и рассчитывается по формуле:

Вычислим Y : Y = λ / μ Y = 2 / 0.8 =2.5

Вычислим P₀ : P₀ = 0.09

Вычислим : =0.4

Таким образом, среднее число машин находящихся в очереди на обслуживании есть 0.4 .

2) Найдем среднее время ожидания в очереди для одной заявки по формуле:

.

=0.2

3)

P_отк=0.07

Вероятность отказа в обслуживании составляет 7%.

Задача

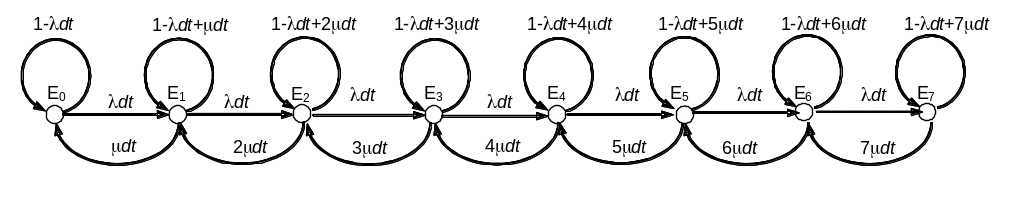
Составим систему уравнений:

Приравняем правые части к нулю:

1. Вероятность того, что абонент не застанет АТС занятой (в системе находятся 6 и менее заявок):

2. Вероятность занятости канала:

3. Среднее число занятых каналов:

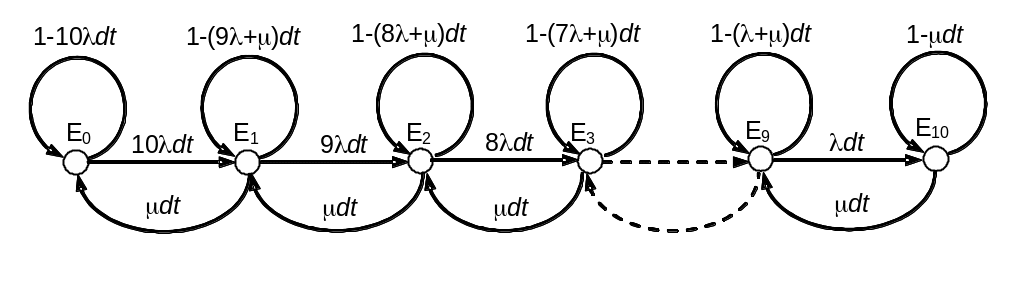
Задача

Данная система является многоканальной СМО с отказами.

Граф переходов:

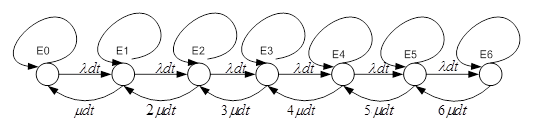
λ = 0.8 – интенсивность поступления заявок

- интенсивность обслуживания

Составим систему уравнений:

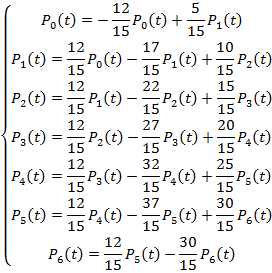
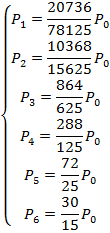
Задача

1. Представить заданную систему как марковскую СМО. Изобразить условную схему СМО, построить граф переходов и систему уравнений состояний. Рассчитать финальные вероятности состояний и указанные в задаче характеристики системы. Линия связи содержит 3 канала. Вызовы принимаются при наличии хотя бы одного канала. Если каналы заняты, вызов получает отказ. Интенсивность потока =0.8 выз/мин. (поток пуассоновский). Средняя продолжительность разговора 1.5 мин. Найти вероятность отказа в обслуживании; среднее число занятых каналов; среднее время пребывания вызовов на станции.

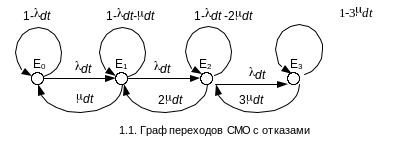
2. 10 рыболовных траулеров обслуживаются плавучей базой. Среднее время плавания равно 3 суткам. На базе имеется 1 причал. Среднее время обслуживания 8 часов. Определить среднюю длину очереди; среднее время простоя траулера.

Задание 3. Рабочий обслуживает группу из 3 станков, каждый из которых останавливается в среднем 2 раза в час. Среднее время переналадки станка 10 мин. Определить среднее количество простаивающих станков; среднее время простоя станка; коэффициент загрузки рабочего.

1. На автозаправочной станцию поступает поток автомашин (пуассоновский) с интенсивностью =1,6 авто/мин. Колонка обслуживает машину в среднем за 1,25 мин. Количество работающих колонок равно 3. Определить: среднее число машин в очереди ; среднее время ожидания в очереди ; вероятность того, что длина очереди не превышает количество колонок.

Решение.

Это задача о многоканальной Системе Массового Обслуживания с ожиданием.

Введем обозначения

λ = 1.6 это интенсивность входного потока

t_об = 1.25 это время обслуживания одной колонкой

одного автомобиля

μ = 1 / t_об среднее число заявок обслуживаемых уз-

лом за единицу времени

S =3 количество колонок

Рассмотрим вероятности переходов при изменении состояний системы.

Изменение состояния:	Вероятность перехода:
-> -> ->

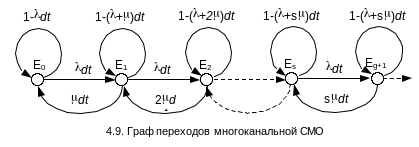
Изобразим соответствующий граф переходов:

1) Найдем среднее число машин в очереди по формуле,

где в свою очередь P₀ есть вероятность простоя узлов обслуживания СМО, когда нет заявок, и рассчитывается по формуле:

Вычислим μ : μ = 1 / t_об μ = 1 / 1.25 =0.8

Вычислим  :  = λ / μ  = 1.6 / 0.8 = 2

Вычислим P₀ : P₀ = 1/9

Вычислим : =8/9=0.89

Таким образом, среднее число машин находящихся в очереди на обслуживании есть 0.89 .

Найдем среднее время ожидания в очереди для одной заявки по формуле

.

=0.56

3) Найдем вероятность того, что длина очереди не превышает количество колонок :

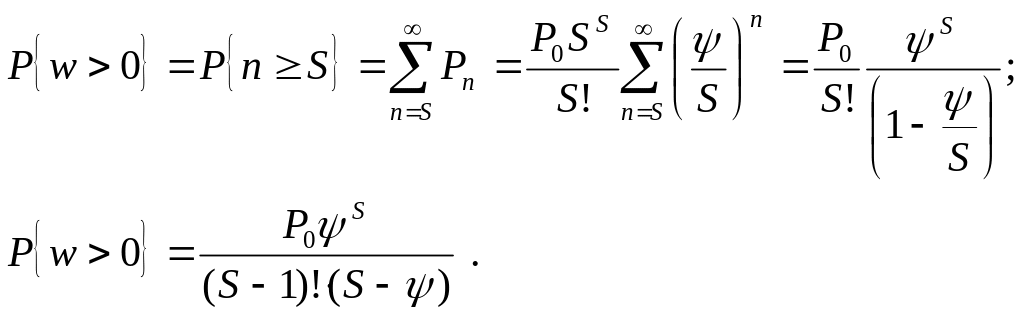
P =0.44

Вероятность того, что длина очереди не превышает количество колонок составляет 44%.

Задача

С целью увеличения дальности беспосадочного полета производится дозаправка самолетов в воздухе. В районе дозаправки постоянно дежурят 4 самолета дозаправщика. Дозаправка длится в среднем 10 минут. Интенсивность полетов такова, что в среднем в район дозаправки прибывают 24 самолета в час. Если дозаправщики заняты, то самолет может ожидать дозаправки в воздухе, ели количество ожидающих самолетов не превышает пяти иначе следует посадка на запасной аэродром

Определить: вероятность того, что самолет будет дозаправлен; среднее число занятых дозаправщиков, среднее время простоя дозаправщика.