3.2 Жидкие провода
Более классическим способом может являться использование эластичных проводников из сплава жидких проводников заключённых в растягивающуюся обкладку (рисунок 28).
В Университете Северной Каролины (США) разработаны электрические провода, которые можно растянуть, увеличив их длину в восемь (!) раз при полном сохранении функциональности.
Для создания «растягивающихся» проводов учёным понадобились тонкие трубочки из сверхэластичного полимера, которые затем были заполнены жидким металлическим сплавом галлия и индия (эвтектический расплав), который является хорошим электрическим проводником. В качестве материала для эластичной изоляционной обкладки был выбран трёхблочный сополимер SEBS.
Рисунок 28 - Жидкий провод в разрезе.
В случае более традиционного подхода к созданию эластичных проводов, основанного на встраивании металла в полимерную матрицу, значительное повышение содержания металла хотя и улучшает проводимость композита, но отрицательно сказывается на его эластичности. Иначе говоря, либо высокая проводимость, либо эластичность, что делает всю затею бессмысленной. В данном исследовании, результаты которого опубликованы в журнале Advanced Functional Materials, использование сплава индия-галлия позволяет довести содержание проводника до 100% и при этом сохранить невероятную эластичность.
Недостатками таких эластичных проводов являются высокая цена сплава индия и галия и проблема вытекания металла при механическом повреждении обкладки [25].
Оптимизация модели под радиопоглощающий материал с динамическими размерами
Следующим этапом нашей работы является зависимость изменения размеров всего РПМ. (размер RSS ячейки и размер диэлектрика). Взятая за основу базовая модель ЧСП с размерами диэлектрика 41,7х41,7х1 мм3 и RSS с ячейкой размера 8,33x8,33x1 мм3 размеры которой, кроме толщины диэлектрика, были увеличены относительно первоначальных значений на 20% и 40%, а количество треугольников компьютерной модели изменилось на 1727 и 3521 единиц соответственно.
Для оптимизации рабочего процесса, была создана переменная «а». А геометрические размеры фигур и их координаты являются функциями, зависимыми от «a». Таким образом, нет необходимости каждый раз заново перестраивать плоскость материала под новый размер (рисунок 29).
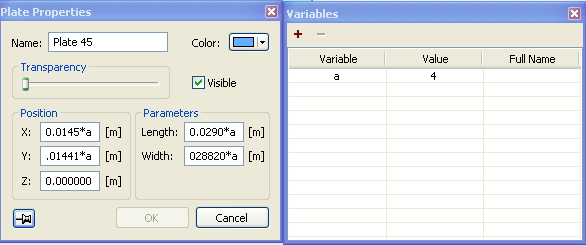
Рисунок 29 – Окно переменных.
На рисунке 30 видно, что изменение размеров приводит к сдвигу резонансной частоты. При увеличении размера РПМ на 20% и 40% резонансная частота сдвигается на частоту 7,75 ГГц и 6,5 ГГц соответственно.
При этом, в случае изменения электродинамических характеристик при растяжении материала, не приведёт к существенному изменению свойств поглощения. В этом мы можем убедиться в таблице 4, где сравнивались уровни обратного рассеяния материала из медных кольцевых щелевых резонаторов и изготовленных из идеального проводника.
Рисунок 30 - Зависимость напряженности рассеянного электрического поля от РПМ от частоты при разных размерах РПМ.