16

Лекція 3 «Методи побудови парної лінійної регресії»

Анотація

«Істинне» рівняння регресії. Парна регресія. Систематична та випадкова складові. Умови Гаусса-Маркова. Гетероскедастичність та гомоскедастичність. Властивості оцінок параметрів регресійного рівняння: незміщеність, обґрунтованість, ефективність та інваріантність. Метод найменших квадратів (МНК). Оцінки найменших квадратів. Верифікація моделі. Стандартна похибка рівняння. Оцінений коефіцієнт детермінації. Перевірка значущості та довірчі інтервали. Прогнозування за лінійною моделлю.

1.1 Регресійна задача для випадку одного фактора

Після кореляційного аналізу проводиться регресійний аналіз, основною задачею якого є дослідження залежності змінної, що вивчається, від різних факторів та відображення їх взаємозв’язку у формі регресійної моделі.

Нехай маємо набір значень двох змінних  – пояснювальна змінна та  – пояснююча змінна, кожна з яких містить n спостережень. Нехай між ними теоретично існує деяка лінійна залежність

, (3.1)

Це рівняння будемо називати «істинним» рівнянням регресії.

Однак в дійсності між змінними спостерігається не настільки жорсткий зв'язок. Окремі спостереження будуть відхилятися від від лінійної залежності в силу різних причин. Враховуючи можливі відхилення лінійне рівняння зв’язку двох змінних (парну регресію) представимо у вигляді

, (3.2)

де  – постійна величина (або вільний член рівняння);

 – коефіцієнт регресії, що визначає нахил лінії. вздовж якої розсіяні дані спостереження;

 – випадкова змінна (випадкова складова, залишок або збурення).

У векторно-матричній формі, співвідношення (14.1) буде мати такий вигляд:

(3.3)

де

.

Випадкова складова відображає той факт, що зміна буде неточно описуватися зміною , оскільки присутні інші фактори, невраховані в даній моделі. Таким чином в рівнянні (3.2) значення кожного спостереження представлено як сума двох частин – систематичної та випадкової . В свою чергу систематичну частину можна представити у вигляді рівняння

. (3.4)

Можна сказати, що загальним моментом для будь-якої економетричної моделі є розбиття залежної змінної на дві частини – пояснену та випадкову.

1.2 Основні передумови методу найменших квадратів (МНК)

Властивості коефіцієнтів регресії істотним чином залежать від властивостей випадкової компоненти. Для того, щоб регресійний аналіз, що базується на звичайному методі найменших квадратів (МНК) давав найкращі із всіх можливі результати, необхідно щоб виконувалися певні умови, які називаються умовами Гаусса-Маркова, а саме:

1. Математичне сподівання випадкових відхилень повинно дорівнювати нулеві (незміщеність оцінок):

. (3.5)

Ця умова вимагає, щоб випадкові відхилення в середньому не впливали на залежну змінну Y, тобто в кожному конкретному спостереженні відхилення може набувати додатні або від’ємні значення, але не повинно спостерігатися систематичне зміщення відхилень в переважній більшості в бік одного знаку.

Із врахуванням вищесказаного, використовуючи рівняння (3.2), будемо мати:

(3.6)

2. Дисперсія випадкових відхилень повинна бути сталою величиною

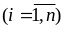, . (3.7)

Ця вимога передбачає, що не зважаючи на те, що при кожному конкретному спостереженні випадкове відхилення може виявитися відносно великим чи малим, це не повинно складати основу для апріорної причини, тобто причини, що не базується на досвіді, що спонукала б велику похибку.

Моделі, для яких виконується умова (3.7), називають гомоскедастичними (рівнозмінними). Моделі, для яких не виконується умова (2) ( ), називають гетероскедастичними.

Величина , звичайно, не відома і одна з задач регресійного аналізу полягає в оцінці стандартного відхилення випадкової складової.

3. Випадкові відхилення та , повинні бути незалежними одне від одного.

Виконання цієї умови припускає, що між будь-якими випадковими відхиленнями відсутній систематичний зв’язок, тобто величина та знак будь-якого випадкового відхилення не буде являтися причиною величини та знаку будь-якого іншого випадкового відхилення. Цю умову можна записати так

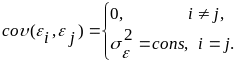(3.8)

Тут є математичний запис коваріаційного (кореляційного) моменту.

4. Випадковий вектор відхилень повинен бути незалежним від регресорів матриці .

Ця умова виконується автоматично, коли пояснюючі змінні не є стохастичними величинами в заданій моделі.

,

бо , а ( не є випадковою величиною).

А також незалежні змінні моделі повинні утворювати лінійно незалежну систему векторів, або, іншими словами, незалежні змінні не повинні бути мультиколінеарними, тобто :

.

де X_k – k-й вектор матриці пояснювальних змінних; X_j – j-й вектор цієї матриці пояснювальних змінних X, .

Поряд з умовами гауса-Маркова зазвичай також припускається, що компоненти випадкового вектора повинні мати нормальний закон розподілу .

Тоді випадковий вектор буде мати нормальний закон розподілу виду .

З теорії ймовірностей відомо (доведено в теоремі Гаусса-Маркова), що коли виконуються перелічені передумови, то отримані за допомогою МНК оцінки параметрів регресійного рівняння є незміщеними, обґрунтованими, ефективними та інваріантними.

Наявність таких властивостей оцінок гарантує, що останні не мають систематичної похибки (незміщеність), надійність їх підвищується зі збільшенням обсягу вибірки (обґрунтованість), вони є найкращими серед інших оцінок параметрів, лінійних відносно ендогенної змінної (ефективність). Крім того, оцінка перетворених параметрів (оцінка функції від параметра) може бути отримана в результаті аналогічного перетворення оцінки параметра (інваріантність).

Зокрема, якщо порушується третя передумова МНК (за наявності автокореляції чи гетероскедастичності), то отримані за цим методом оцінки втрачають властивість ефективності, хоча залишаються незміщеними та обґрунтованими. Якщо порушується четверта передумова, тобто між змінними існують мультиколінеарні зв’язки, це призводить до зміщення МНК-оцінок. Застосування моделей, що мають зміщені чи неефективні оцінки, втрачає сенс.