Суть та наслідки гетероскедастичності. Методи виявлення та усунення з моделі ознаки гетероскедастичності.
Чи можливо прогнозування результуючого показника при наявності гетероскедастичності?
Найкращий незміщений лінійний точковий прогноз у випадку гетероскедастичності обчислюється за наступною залежністю :
,
( 27 )
де:
B – вектор оцінок параметрів моделі,
отриманих узагальненим методом найменших
квадратів (УМНК);
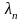– останній параметр з матриці S (для
останнього спостереження у вибірці);
- залишок в останньому спостережені,
обчислений для моделі, параметри якої
оцінені на основі 1МНК;
- вектор прогнозних значень пояснюючих
змінних моделі.
Інтервальні прогнози у випадку гетероскедастичності обчислюються за наступними залежностями :
інтервальний прогноз для індивідуального значення залежної змінної
; (
28 )
інтервальний прогноз для математичного сподівання залежної змінної
. (
29 )
Узагальнений метод найменших квадратів (метод Ейткена): сутність і використання.
За наявності гетероскедастичності для оцінювання параметрів моделі доцільно застосовувати узагальнений метод найменших квадратів (метод Ейткена), вектор оцінювання якого має вигляд:
.
Вектор а містить незміщену лінійну оцінку параметрів моделі, яка має найменшу дисперсію і матрицю коваріацій:
.
Для отримання УМНК-оцінок необхідно знати коваріаційну матрицю S вектора похибок, яка на практиці дуже рідко відома. Тому природно спершу оцінити матрицю S, а потім застосувати її оцінку у формулах. Цей підхід є суттю УМНК.
Оскільки явище гетероскедастичності пов’язане лише з тим, що змінюються дисперсії залишків, а коваріація між ними відсутня, то матриця S має бути діагональною, а саме:
Щоб пояснити, чому саме такий вигляд має ця матриця, потрібно ще раз наголосити: за наявності гетероскедастичності для певних вихідних даних одна (або кілька) пояснювальних змінних можуть різко змінюватись від одного спостереження до іншого, тоді як залежна змінна має такі самі коливання, як і для попередніх спостережень.
Але це означає, що дисперсія залишків, яка змінюватиметься від одного спостереження до іншого (чи для групи спостережень), може бути пропорційною до величини пояснювальної змінної X (або до її квадрата), яка зумовлює гетероскедастичність, або пропорційною до квадрата залишків.
Звідси в матриці S значення можна обчислити, користуючись гіпотезами:
а) , тобто дисперсія залишків пропорційна до зміни пояснювальної змінної ;
б) , тобто зміна дисперсії пропорційна до зміни квадрата пояснювальної змінної ( );
в) , тобто дисперсія залишків пропорційна до зміни квадрата залишків за модулем.
Для першої гіпотези:
Для другої гіпотези:
Для третьої гіпотези: або , або .
Оскільки матриця S – симетрична і додатньо визначена, то при , матриця P має вигляд:
.
При цьому коефіцієнт детермінації не може бути задовільною мірою якості моделі у випадку застосування УМНК. У загальному випадку його значення навіть не повинно перебувати в межах , а додавання чи вилучення незалежної змінної не обов’язково зумовлює його збільшення чи зменшення.