9. Яким чином здійснюється перевірка статистичної значущості параметрів та перевірка загальної якості множинної регресії?

Якість моделі регресії перевіряється на основі аналізу залишків регресії . Аналіз залишків дозволяє отримати уявлення про те, наскільки добре підібрана модель і наскільки правильно вибраний метод оцінки коефіцієнтів. Згідно загальним припущенням регресійного аналізу, залишки повинні вести себе як незалежні однаково розподілені випадкові величини. Дослідження доцільно починати з вивчення графіку залишків. Він може показати наявність якої-небудь залежності, що не врахована в моделі. Графік добре показує і викиди, яких потрібно позбавлятися.

Якість моделі оцінюється за наступними напрямками (аналогічно до парної регресії):

• перевірка якості рівняння регресії (індекс кореляції та коефіцієнт детермінації);

• перевірка значимості рівняння регресії (критерій Фішера);

• аналіз статистичної значущості параметрів моделі (t-критерій);

• перевірка виконання передумов МНК.

Умови, що необхідні для отримання незміщених, спроможних та ефективних оцінок, представляють собою передумови МНК. Виконання умови рівності нулеві математичного очікування залишків забезпечується завжди при використанні МНК для лінійних моделей. Передумова про нормальний розподіл залишків дозволяє проводити перевірку параметрів регресії за допомогою критеріїв t та F. разом з тим оцінки регресії, отримані методом МНК, мають добрі властивості навіть при відсутності нормального розподілу залишків. Таким чином, найважливішими є виконання умови незалежності та умови гомоскедастичності.

10. Як визначаються дисперсія залишків, загальна дисперсія і дисперсія регресії? Який між ними зв’язок?

11. Яким чином оцінюється адекватність моделі?

Модель вважається гарною зі статистичної точки зору, якщо вона адекватна і достатньо точна.

1. Для перевірки адекватності моделі реальному явищу досліджується ряд залишків, тобто розбіжностей рівнів, розрахованих по моделі, та фактичних спостережень.

а) Перевірка рівності математичного очікування рівнів ряду залишків нулю здійснюється в ході перевірки відповідної нульової гіпотези . З цією метою будується t-статистика:

(5.17)

де  – середнє арифметичне значення рівнів ряду залишків;

S – середньоквадратичне відхилення для цієї послідовності, розраховане для малої вибірки.

В подальшому дане розраховане значення порівнюють з табличним і роблять висновок про прийняття або відхилення гіпотези.

б) Перевірка умови випадковості виникнення окремих відхилень від тренду.

в) Перевірка умови незалежності, або наявності автокорреляції у відхиленнях від моделі росту (буде розглянуто пізніше).

г) Відповідність ряду залишків нормальному закону розподілу.

12. Яким чином оцінюється точність моделі?

2. Оцінка точності моделі. В статистичному аналізі широко відомо велика кількість характеристик точності. Найбільш часто, окрім середньоквадратичного відхилення, використовують:

• максимальна за абсолютною величиною похибка

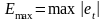; (5.18)

• відносна максимальна похибка

; (5.19)

• середня по модулю похибка

; (5.20)

• середня по модулю відносна похибка

. (5.21)

Кращою за точністю вважається та модель, у якої всі перелічені характеристики мають меншу величину.