2

Лабораторна робота №3

«Побудова та аналіз моделі множинної нелінійної регресії»

Мета роботи: побудувати та проаналізувати модель множинної нелінійної регресії.

Зміст роботи: проведення параметризації рівняння регресії за двома припущеннями – стохастична залежність між факторами і результуючим показником має лінійний та нелінійний вигляд. Оцінка статистичної значимості побудованих регресій та їх параметрів. Вибір регресії, що краще відображає початкові статистичні дані, і здійснення прогнозу на основі обраної моделі.

Завдання до роботи:

1. Побудувати лінійне рівняння множинної регресії Y від факторів X₁ та X₂. За допомогою t-критерію оцінити статистичну значимість коефіцієнтів лінійної моделі множинної регресії.

2. Знайти коефіцієнти парної, частинної та множинної кореляції. Проаналізувати їх. Зробити висновок про силу впливу факторів на результат і можливості мультиколінеарності факторів.

3. Знайти скорегований коефіцієнт множинної детермінації. Порівняти його з нескорегованим (загальним) коефіцієнтом детермінації. За допомогою -критерію Фішера оцінити статистичну надійність рівняння регресії і коефіцієнта детермінації. Оцінити якість рівняння регресії через середню похибку апроксимації.

4. Припустивши, що стохастична залежність між факторами X₁, X₂ та показником Y має нелінійний вигляд, привести регресію до лінійного вигляду.

5. Оцінити параметри отриманого лінійного рівняння регресії.

6. Використовуючи критерій Фішера, необхідно оцінити з надійністю p=0,95 адекватність прийнятої математичної моделі статистичним даним.

При виконанні завдань 1-6 використати надбудову «Аналіз даних» чи функції MS Excel ЛИНЕЙН(), КОРРЕЛ(), а також функції СТЬЮДРАСПОБР(), FРАСПРОБР() тощо.

7. Вибрати кращу з двох оцінених моделей і знайти оцінки прогнозу за нею та з надійністю p=0,95 його довірчий інтервал.

8. Побудувати поле кореляції та графік лінії регресії.

9. Зробити висновки щодо взаємозв’язку факторів та адекватності побудованого регресійного рівняння.

Для напряму «Економічна кібернетика»: виконати всі дії паралельно в ПП MathCAD або Statistica.

Початкові дані:

На основі статистичних даних показника Y і факторів X₁, X₂ (табл. 1) та враховуючи вид нелінійної функції (табл. 2), що за припущенням описує залежність між факторами і результуючим показником, виконати завдання до роботи.

Таблиця 1 – Значення факторів X₁, X₂ та показника Y (згідно варіанту)

№ варі-анту	показник	Номер року
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	X1	0,43	0,78	0,91	1,03	1,29	1,30	1,62	1,70	1,71	1,77	1,99	2,06	2,42	2,63	2,89
	X2	5,12	5,09	4,70	4,23	3,87	3,43	3,26	2,85	2,59	2,50	2,11	1,73	1,35	0,87	0,48
	Y	21,22	23,91	21,78	17,83	17,36	12,70	14,63	11,08	9,82	10,20	8,92	7,90	8,94	6,30	?
2	X1	5,12	5,36	7,15	8,73	9,96	10,66	11,79	12,08	12,17	13,67	15,12	15,96	18,47	20,08	20,84
	X2	3,02	2,89	2,86	2,76	2,61	2,41	2,36	2,32	2,15	2,14	2,09	1,86	1,82	1,73	1,67
	Y	31,39	31,68	43,69	54,43	59,50	59,16	66,65	67,91	62,26	73,34	80,70	77,80	91,17	97,43	?
3	X1	0,51	0,63	0,88	1,11	1,25	1,36	1,50	1,53	1,78	2,09	2,20	2,25	2,34	2,56	2,57
	X2	24,15	22,91	22,77	20,78	19,93	19,50	19,38	18,72	18,33	18,16	16,16	14,46	12,84	11,38	10,32
	Y	972,26	406,1	150,32	87,03	65,67	56 ,43	48,17	45,75	38,23	31,91	27,19	25,65	21,79	19,03	?
4	X1	15,78	15,26	13,43	13,07	12,13	11,52	11,35	10,22	8,62	8,00	7,65	7,60	6,09	5,45	0,51
	X2	0,49	0,81	1,14	1,30	1,55	1,65	1,73	2,11	2,31	2,50	2,77	2,80	3,08	3,29	3,50
	Y	41,11	42,82	40,16	39,65	37,51	37,45	36,38	36,96	31,18	30,73	29,59	30,87	24,49	23,61	?
5	X1	5,12	5,70	6,50	7,24	7,87	8,15	8,41	9,26	9,66	10,02	10,25	10,35	10,38	10,58	10,83
	X2	12,11	11,86	11,80	11,71	11,23	10,88	10,30	9,57	9,56	9,46	9,24	8,54	8,13	7,51	6,77
	Y	11,78	9,41	8,74	9,06	10,22	10,31	8,62	8,67	9,01	9,99	7,76	9,87	10,96	12,11	?
6	X1	1,12	1,39	1,53	1,96	2,20	2,32	2,76	2,97	3,19	3,20	3,44	3,67	4,05	4,55	4,98
	X2	13,13	15,48	15,58	17,26	17,44	19,72	21,51	23,50	24,93	26,85	29,30	29,44	31,93	33,51	34,02
	Y	49,48	54,28	54,24	58, 46	59,08	64,84	70,09	76,45	80,95	85,00	92,65	92,68	99,92	104,3	?
7	X1	50,76	58,53	97,01	126,17	143,64	152,62	189,46	198,89	231,0	243,4	261,7	264,13	269,0	284,1	298,3
	X2	52,07	57,44	73, 24	74,97	83,16	88,94	132,44	155,39	193,8	231,0	273,9	308,23	323,4	361,4	400,9
	Y	16,90	18,12	18,98	19,57	19,81	20,61	21,19	21,82	22,3	22,7	22,7	23,56	23,0	23,9	?
8	X1	52,06	73,80	73,85	84,28	98,64	103,30	105,39	108,43	114,5	148,8	181,3	206,63	236,0	274,7	293,6
	X2	25,17	27,33	26,17	27,39	27,17	27,20	28,17	30,47	29,17	30,48	30,17	31,92	31,17	33,95	32,17
	Y	66,26	73,07	70,62	73,88	74,16	74,75	75,59	80,15	79,34	82,63	81,01	86,12	84,06	90,04	?
9	X1	3,52	4,676	5,507	7,729	7,995	10,07	12,98	14,84	17,83	18,67	21,15	23,12	25,09	27,77	29,67
	X2	52,06	53,10	53,62	55,07	57,63	58,86	59,28	62,22	65,95	67,37	69,86	70,54	74,25	75,26	77,69
	Y	20,99	19,23	19,53	18,1	20,16	19,92	19,27	18,28	18,53	18,17	18,87	19,5	19,22	19,19	?
10	X1	52,06	52,63	54,1	57,66	58,47	61,71	66,06	68,23	72,11	72,44	74,77	78,6	84,53	84,6	85,02
	X2	21,06	22,85	24,73	29	31,07	35,48	35,9	39,33	41,57	43,36	46,26	49,31	53,1	53,64	56,17
	Y	5,625	5,509	5,645	58,12	5,997	6,092	6,11	6,463	63,56	6,626	6,431_	6,568	6,835	7,129	?
11	X1	0,52	5,319	10,02	14,61	20,11	20,17	25,3	27,61	30,25	32,13	37,38	41,01	44,43	47,47	52,25
	X2	2,42	7,024	11,38	14,3	15,34	17,31	21,78	24,69	29,48	32,98	35,63	40,52	41,4	44,33	46,39
	Y	2,399	0,961	0,593	0,579	0,557	0,409	0,367	0,411	0,336	0,365	0,245	0,199	0,359	0,318	?
12	X1	46,23	49,5	51,28	51,3	53,22	54,48	57,23	59,64	64,01	65,38	66,73	67,46	70,16	70,58	71,36
	X2	25,65	33,44	38,33	45,77	53,06	55,48	62,71	68,42	68,94	69,58	73,28	79,46	82,52	87,19	93,83
	Y	5,25	5,593	5,016	5,128	5,056	5,89	5,323	5,312	5,977	5,363	5,984	5,692	5,402	5,28	?
13	X1	3,05	3,78	4,119	4,629	6,053	7,234	7,535	9,434	9,658	10,05	11,04	12,16	13,14	13,73	13,86
	X2	4,26	5,326	7,272	7,793	6,679	10,55	12	13,72	14,63	14,75	16,58	17,25	18,65	19,55	20,12
	Y	2,57	3,71	1,822	2,595	5,662	6,298	4,303	6,635	5,848	7,223	6,645	73	7,569	7,486	?
14	X1	52,07	52,74	56,49	63	67,17	73,05	77,25	83,86	87,47	89 11	95,42	101,9	104,2	109,6	112,6
	X2	35,55	40,23	41,59	43,75	46,95	50,17	51,74	59,14	63,24	68.21	74,64	82,28	87,33	95,06	96,19
	Y	9,794	9,943	9,354	9,837	10,09	10,69	10,92	11,31	12,28	11 57	12,81	12,4	13,39	13,01	?
15	X1	52,07	58,76	64,73	68,06	69,3	72,78	77,07	77,32	82,93	83,91	88,4	90,29	93,39	99,93	102,3
	X2	34,45	35,22	37,25	39,59	41,01	41,55	44,26	44,41	47,84	48,06	46,83	52,83	54,57	56,89	59,91
	Y	31,4	32,38	34,27	35,48	35,81	35,66	37,7	36,34	38,83	39,17	39,93	39,77	40,6	40,56	?
16	X1	25,25	27,9	31,36	32,55	38,27	42,25	43,94	45,93	46,21	47,87	50,91	56,75	58,27	62,89	63,97
	X2	31,34	32,61	34,66	35,94	37,61	39,95	41,92	43,03	43,4	44,29	44,58	44,79	47,06	47,58	47,72
	Y	15,65	17,5	17,88	17,4	18,09	18,47	20,34	19,33	19,33	20,27	21,05	20,92	21,63	22,05	?
17	X1	2,31	5,376	6,344	8,85	8,943	9,951	11,04	12,49	14,23	1679	20,03	23,81	27,08	27,58	31,07
	X2	0,31	0,39	0,415	0,471	0,514	0,807	0,902	0,965	1,209	1,269	1,434	1,722	1,762	1,91	2,186
	Y	4,309	4,585	5,107	5,884	6,455	6,99	7,299	7,532	8,231	9,816	10,98	13,29	14,39	14,11	?

Таблиця 2 – Вид нелінійної функції, що за припущенням описує залежність між факторами і результуючим показником (згідно варіанту)

№ варіанту	Вид нелінійної функції	№ варіанту	Вид нелінійної функції
1		10
2		11
3		12
4		13
5		14
6		15
7		16
8		17
9

Вимоги до звіту: назва, тема, мета, завдання, розрахункові формули. Результати аналітичного розв’язання задачі та комп’ютерного у вигляді таблиці MS Excel з вихідними умовами експерименту, таблиці MS Excel з результатами обчислень, висновок про отримані результати. Опис інструментів та функцій MS Excel, що використовувались при вирішенні задачі. Короткий опис технології вирішення задачі в MS Excel (для напряму «Економічна кібернетика» – опис технології вирішення задачі в ПП MathCAD або Statistica).

МЕТОДИЧНІ ВКАЗІВКИ ДО РОЗВ’ЯЗАННЯ ЗАДАЧІ

Приклад. Проаналізувати наступні статистичні дані:

№ спостереження				№ спостереження
1	7,0	3,9	10,0	11	9,0	6,0	21,0
2	7,0	3,9	14,0	12	11,0	6,4	22,0
3	7,0	3,7	15,0	13	9,0	6,8	22,0
4	7,0	4,0	16,0	14	11,0	7,2	25,0
5	7,0	3,8	17,0	15	12,0	8,0	28,0
6	7,0	4,8	19,0	16	12,0	8,2	29,0
7	8,0	5,4	19,0	17	12,0	8,1	30,0
8	8,0	4,4	20,0	18	12,0	8,5	31,0
9	8,0	5,3	20,0	19	14,0	9,6	32,0
10	10,0	6,8	20,0	20	14,0	9,0	36,0

Розв’язання

1. Розрахуємо параметри лінійного рівняння множинної регресії.

.

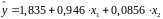Порівняти вплив факторів на результат можна за допомогою середніх коефіцієнтів еластичності:

.

Розрахуємо:

; .

Тобто збільшення факторів X₁ та X₂ на 1% збільшує результат на 0,61% или 0,20% відповідно. Таким чином, підтверджується більший вплив на результат фактора , ніж фактора .

2. Розрахуємо коефіцієнти парної кореляції:

; ; .

Вони вказують на значно сильний зв'язок кожного фактору з результатом, а також високу міжфакторну залежність (фактори і явно колінеарні, так як ). При такій сильній міжфакторній залежності рекомендується один з факторів виключити з розгляду.

Частинні коефіцієнти кореляції характеризують тісноту зв’язку між результатом та відповідними факторами при елімінуванні (виключенні впливу) інших факторів, включених в рівняння регресії.

При двох факторах частинні коефіцієнти кореляції розраховуються наступним чином

;

.

Якщо порівнювати коефіцієнти парної та частинної кореляції, то можна побачити, що через високу між факторну залежність коефіцієнти парної кореляції дають завищену оцінку тісноти зв’язку. Саме через цю причину рекомендується при наявності сильної колінеарності факторів виключати з дослідження той фактор, у якого тіснота парної залежності менша, ніж тіснота міжфакторного зв’язку.

Коефіцієнт множинної кореляції

показує сильний зв'язок всього набору факторів з результатом.

2. Нескорегований коефіцієнт множинної детермінації оцінює частку варіації результату за рахунок представлених у рівнянні факторів в загальній варіації результату. Тут ця частка складає 94,7% і вказує на високу ступінь обслуговування варіації результату варіації факторів, іншими словами – на досить тісний зв'язок факторів з результатом.

Скорегований коефіцієнт множинної детермінації

визначає тісноту зв’язку з урахуванням ступенів свободи загальної та залишкової дисперсії. Він дає таку оцінку тісноту зв’язку, яка не залежить від числа факторів, і тому може порівнюватися по різним моделям з різним числом факторів. Обидва коефіцієнти вказують на досить високу (більш 94%) детермінованість результату у моделі факторами і .

Оцінку надійності рівняння регресії в цілому та показника тісноти зв’язку дає -критерій Фішера:

.

В даному випадку фактичне значення -критерію Фішера:

.

Отримали, що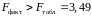 (при ), тобто ймовірність випадково отримати таке значення -критерію не перевищує допустимий рівень . Відповідно, отримане значення не випадкове, воно сформувалось під впливом істотних факторів , тобто підтверджується статистична значимість всього рівняння та показника тісноти зв’язку .

Загальний висновок полягає в тому, що множинна модель з факторами та з , включає неінформативний фактор . Якщо виключити фактор , то можна обмежитися рівнянням парної регресії:

, .

4. Вводиться гіпотеза, що між факторами X₁, X₂ та показником Y існує така стохастична залежність:

.

Для приведення регресії до лінійного виду пропотенціюємо регресію та зробимо заміну величин

, , .

Отримаємо наступне рівняння лінійної регресії:

.

5. Для оцінки параметрів a₀, a₁, a₂ використаємо метод найменших квадратів (МНК).

Після оцінки параметрів a₀, a₁, a₂ знаходимо розрахункові значення .

6. Адекватність прийнятої моделі експериментальним даним визначається за критерієм Фішера , де R² – коефіцієнт детермінації. Якщо F_розр > F_табл , то з надійністю p=0,95 можна вважати, що прийнята економетрична модель адекватна експериментальним даним і її можна використовувати для аналізу економічних процесів, робити висновки про розвиток економічного процесу в майбутньому.

Контрольні питання:

1. Назвіть два класи нелінійних регресій.

При вивченні залежностей економічних показників на основі реальних статистичних даних з використанням апарату теорії ймовірностей та математичної статистики можна зробити висновки, що лінійні залежності зустрічаються не так часто. Їх використовують лише як частковий випадок для зручності та наочності розгляду економічного процесу. Частіше зустрічаються моделі,які відображають економічні процеси у вигляді нелінійної залежності. Існує також так звана кускова функція, яка на різних ділянках області визначення може бути задана різними аналітичними виразами.

Якщо між економічними явищами існують нелінійні відношення, то вони виражаються за допомогою відповідних нелінійних функцій.

Розрізняють два класи нелінійних регресій:

1) нелінійні відносно пояснюючих змінних, однак лінійні по параметрам, що оцінюються;

2) нелінійні по параметрам, що оцінюються.

2. Наведіть приклади регресій, нелінійних відносно пояснюючих змінних, однак лінійні по параметрам, що оцінюються.

Клас регресій нелінійних відносно пояснюючих змінних, однак лінійних по параметрам, що оцінюються, включає рівняння, в яких залежна змінна лінійно пов’язана з параметрами. Приклад таких регресій можуть слугувати:

• поліноми різних ступенів

; (5.1)

• рівностороння гіпербола

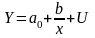. (5.2)

3. Наведіть приклади регресій, нелінійних по параметрам, що оцінюються.

До класу регресій, нелінійних по параметрам, що оцінюються, відносяться рівняння, в яких залежна змінна нелінійно пов’язана з параметрами. Прикладом таких регресій є функції:

• степенева: ;

• показникові: ;

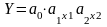• експоненціальні: .

4. Яким чином нелінійні відносно пояснюючих змінних рівняння регресій можуть бути зведені до лінійних?

При оцінці параметрів регресії, нелінійних по пояснюючим змінним, використовується метод заміни змінних. Суть його полягає в заміні нелінійних пояснюючих змінних новими лінійними змінними, в результаті чого нелінійна регресія зводиться до лінійної. До нової, перетвореної регресії може бути застосований звичайний МНК.

Наприклад, у випадку поліноміальної моделі з декількома пояснюючими змінними

(5.3)

заміна , , , ... призводить до лінійної регресійної моделі.

5. Яким чином нелінійні по параметрам рівняння регресій можуть бути зведені до лінійних?

Якщо нелінійна модель внутрішньо лінійна, то вона за допомогою відповідних перетворень може бути приведена до лінійного виду (наприклад, логарифмуванням). Якщо ж нелінійна функція внутрішньо нелінійна, то вона не може бути зведена до лінійної функції і для оцінки її параметрів використовують ітеративні процедури, успішність яких залежить від виду рівняння та особливостей ітеративного підходу, що застосовується.

Прикладом регресії, що є внутрішньо лінійної є регресія попиту (Y) від загального доходу (z) та ціни цього товару (p):

. (5.4)

Подібні залежності між показником Y та m факторами Z₁, Z₂, ..., Z_m записуються у вигляді

(5.5)

і за допомогою логарифмічного перетворення

(5.6)

зводяться до лінійної по параметрам регресії. Визначення

, , , ..., (5.7)

призводять до лінійної регресійної моделі

. (5.8)

Після оцінювання лінійної моделі (5.8) за допомогою відношень (5.7) можна знайти оцінену регресію для моделі (5.5):

. (5.9)

Моделі виду (5.5) отримали широке розповсюдження при економетричному моделюванні. Це пов’язано з тим, що параметри такої моделі мають змістовну економічну інтерпретацію. З (5.5) випливає, що

, (5.10)

тобто параметр a_i представляє собою коефіцієнт еластичності показника Y по змінній x_i.

Для моделей виду

(5.11)

також використовується логарифмічне перетворення, оскільки визначення , , , ..., приводять їх до лінійної регресії (5.8).

Вибір аналітичної форми дослідження моделі може здійснюватися на основі апріорної інформації про залежність та на основі графіків розкиду емпіричних точок.

6. Яка нелінійна модель називається внутрішньо лінійною?

- нелінійні моделі внутрішньо лінійні, тобто ті, котрі шляхом перетворень можуть бути приведені до поліноміальних лінійних:

- нелінійні моделі внутрішньо не лінійні:

,