11. Параўнанні з невядомымі. Лінейныя параўнанні

Нях. 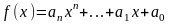– паліном з цэлымі каэф-мі. Разгл. параўнанне (*). Паставім задачу: знаходжанне мн-ва ўсіх , якія задав-ць пар-ню (*).

Т. Калі нейкі цэлы лік а задав-е пар-ню (*), то увесь клас 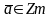складаецца з лікаў, якія задав-ць пар-ню (*).

Вынік. Або пар-не (*) не мае рашэнняў, або мае бясконца многа рашэнняў.

Азн. Рашэннем пар-ня (*) наз. клас па 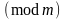, які складаецца з лікаў задавальняючых гэтаму пар-ню. Цэлы лік х0 – раш-не  ах0  b (mod m).

Пр. 1 . У поўнай сіс-ме рэштаў па : -5,-4,...,5 толькі 5 задав-е пар-ню, г. зн., што пар-не мае 1 рашэнне: . Адказ: .

Азн. Пар-не выгляду: 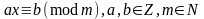, дзе а (1) – пар-не 1-й ступені з адной зменнай (лінейнае пар-не).

Ул. Калі х0 – раш-не (1) і у0  х0 (mod m)  у0 – раш-не (1).

□ у0  х0 (mod m); ау0  ах0 (mod m); але ах0  b (mod m)  х0 – раш-не  - таксама раш-не. ■

Т. калі , тады (1) мае адзінае рашэнне (па mod m).

□ 1) (па крытэрыю узаемапр. лікаў)  u, v а∙u+m∙v  а∙u1 (mod m)  u – рашэнне (1).

2) няхай х1, х2 – раш-не (1)  ах1  а х2 (mod m), але  х1  х2 (mod m)  х1, х2 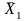 (класу раш-няў). ■

Т. Калі

1) (1) мае рашэнні толькі тады, калі .

2) , тады (1) мае d рашэнняў ў сэнсе класа па .

□ 1) х0 – раш-не (1)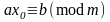  ах0 - b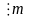  ах0 - b=m∙t; b= ах0 - m∙t

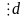
2) па ул-сці пар-ня а=da1; m=dm1; b=db1. da1x  db1x (mod dm1), падзелім на d: a1x = b1 (mod m1), але (a1;m1)=1.

Ўсе раш-ні выглядаюць так: х0 - m1∙t .

t = d ∙s+r (r=0,1,…d-1).

х0 + m1 ∙r+( dm1)∙s ; х0 + m1 ∙r + ms, sZ – запісана r класаў па mod m. Пакажам, што класы розныя. х0 + m1 ∙r1 = х0 + m1 ∙r2 ; . х0 + m1 ∙r1 - (х0 + m1 ∙r2) ; m1(r1-r2) ; магчыма калі r1=r2. ■

Пр. 2 Рашыць пар-не: .

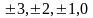. У поўнай с-ме рэштаў па толькі 3 задав. нашаму пар-ню яно мае адзінае рашэнне: .

12. Пераўтварэнне простага дробу ў дзесятковы і вызначэнне даўжыні

перыяду дзесятковага дробу

Азн. Кожны рэчаісны лік выяўляецца бясконц. дзесятк. дробам: ± , дзе ;   m>k am9. Азн. Бяск. дзес. дроб наз. перыядычным, калі цэлыя лікі 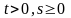, што і абазначаецца (1) . Азн. Калі ў (1) можна ўзяць s=0 маем чысты перыяд. дзесятк. дроб. Азн. Найм. з такіх лікаў s наз. даўжыней перыяду дзес. дробу. Азн. Перыяд. дроб наз. цалкам перыядычным, калі м. узяць . Азн. Перыяд. дроб наз. змешана перыяд., калі нельга ўзяць . Азн. Нях. 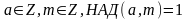. Парадкам ліку а па наз. такі лік , што , але 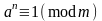. Г. зн., што n – найм. нат. лік, такі, што . Абазн. .

Пр. 1 З-ці парадак ліку 3 па . Маем: , , , , .

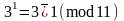Т.  рац. лік выяўляецца перыяд. дз. дробам.

Т. канечным дзес. дроб з’яўляецца выяўленнем 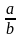– нескарач. дробу, у якога ўсе простыя дзельнікі назоўніка ўтрымл. 2 і 5. □

- рац. дроб, усе простыя дзельнікі наз-ка - 2 і 5. Пасля скарачэння ўсе простыя дзельнікі наз-ка захав-ца. ■

Т. Нескар. дроб выяўл-ца чыстым дзес. перыяд. дробам  (b;10)=1.

Т. Нескар. дроб выяўл-ца змешаным пер. дзесят. дробам  у назоўніка ёсць просты дзельнік 2 ці 5 і ёсць просты дзельнік 2 ці 5.

Т. Нескар. дроб , калі (b;10) 1 і  просты дзельнік p назоўніка, 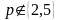, выяўл-ца бяск. змешан. перыяд. дзес. дробам, у якога , дзе . □

по Т.1( нескар. дроб , калі (b;10) =1ён выяўл. чыст. пер. дробам з даўжыней перыяду ) ( - выяўл-ца чыстым пер. дз. дробам с перыядам .

Калі падзел. ( на бяск. дз. пер. дроб з перыядам t і гэты дроб не м.б. чыстым, бо не задавальняе Т.1. ■

Т. 0, (а1…аt) з’яўл. выяўленнем дробу .

Т. Змешаны дз. пер. дроб з’яўл-ца выяўл-нем рац. дроба

.

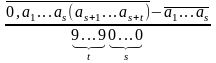Пр. 1) , 2) , 3) .