27. Магутнасць мноства. Незлічонасць мноства сапраўдных лікаў

АЗН: Магутнасцю концага мноства наз-ца лік яго элементаў. Калі мноства бясконцае, то лік яго бясконцы і таму нельга параўнаць у якога з бясконцых мностваў "больш элементаў". У сувязі з гэтым існуе паняцце магутнасці бясконцага мноства, якое дазваляе параўнаць бясконцыя мноствы.

– эквівалентнаcць.

АЗН: Усе мн-вы разаб'ем на классы эквівалентных паміж сабой мн-ваў. Гэтыя класы не перасякаюцца. Магутнасцю мн-ва А наз-ца той клас эквівалентных мностваў, які ўтрымлівае мн-ва А і абазн. . А={5,7,8}. =3.

АЗН: Калі мн-ва А з'яў-ца эквівалентным мн-ву N натуральных лікаў, то мн-ва А наз-ца злічальным. Злічальнае мн-ва заўсёды бясконцае і ўсе яго элементы магчыма занумераваць.

АЗН: Бясконцае мн-ва, якое не з'яў. злічаным наз-ца незлічаным.

Тэарэма: Усе прамежкі лікавай прамой эквівалентны паміж сабой, г.зн яны раўнамагутныя.

Тэарэма: Мноства сапраўдных лікаў R з'яў. незлічаным мн-вам, г.зн. яно бясконцае і не з'яў. злічальным.

Доказ: Т.я мн-ва R эквівалентна любому прамежку, то дастаткова даказаць, што адр-к [0;1] з'яў. незлічаным мн-вам.

Т.я , нам дастаткова дак-ць, што (т.я. з усіх бясконцых мн-ваў наіменшую магутнасць мае злічальнае мноства). Дак-ам ад працілеглага, дапусцім

Т.я мн-ва [0;1] злічальнае, то яго элементы можна занумераваць . Раздзелім адрэзак на тры роўныя часткі і праз І₁ абазн. тую частку, якая не утрымлівае . Адр-к І₁ зноў раздзелім на тры роўныя часткі і праз І₂ абазн. тую частку, якая не утрымлівае . Гэты працэс працягнем неабмежавана. Зн., атрымаем пасл-ць укладзеных адр-каў Пры гэтым іх даўжыні імкнуцца да 0. . Тады па прынцыпу Кантара ўкладзенных адрэзкаў існуе пункт (пры гэтым адзіны), які належыць усім адрэзкам гэтай пасл-ці. Але ..., Т.ч., п. х^* – не занумераваны. Супярэчнасць. Зн., адр-к [0;1] з'яў. незлічаным мн-вам, зн., R з'яў. незлічаным мн-вам.

АЗН.: Магутнасць мн-ва R сапраўдных лікаў наз-ца магутнасцю кантынуума і абазн. літірай с.

1.Усе прамежкі лікавай прамой маюць магутнасць кантынуума.

2.Аб'яднанне концага мноства мностваў магутнасці кантынуума ёсць мноства магутнасці кантынуума. магутнасці кантынуума.

3.Калі да мноства магутнасці кантынуума дабавіць злічальнае мн-ва або адняць ад яго злічальнае мн-ва, то атрымаецца мн-ва магутнасці кантынуума.)

28. Показательная функция комплексной переменной. Эйлеровы формулы

Формулы Эйлера. Рассмотрим функцию: , x- действительное число.

Опр.:

-Фомулы Эйлера.

Можем рассмотреть другие пары: (связь между sin и cos)

--Формулы Эйлера.

Показательная форма записи комплексныхчисел:

Опр.: взаимно однозначное отображение области D на область Е наз.канформным,если:

1. углы между линиями их образов равны;

2. коэффициент растяженияв пункте не зависит от направления.

Если ф. w=f(z) –аналитична в области D, f’(z)0, тогда она осуществляет камфорное отображение области D на некоторую область Е.

Рассмотрим w=f(z)=e^z- аналитическую функцию для zС.

w’=f’(z)=e^z0 На плоскости z возмем полосу D={z:0<Imz<2}

Канформные отображения, которые осуществляются с помощью этой функции:

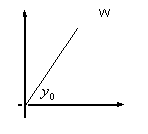
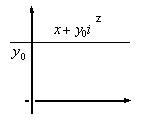Показательная ф-ция отображает горизонтальные прямые . Образом этой прямой является открытый луч .

В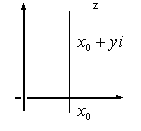 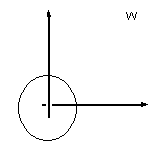ертикальные прямые отображает в окружность радиуса с центром в начале координат.

П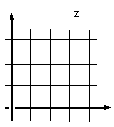 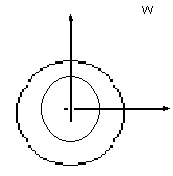оэтому сетка горизонтальных и вертикальных прямых отображается в сетку, кот. состоит из лучей и окружностей.

Экспаоента w=e^x камфорна отображает горизонтальную полосу 0<Imz<2 на всю плоскасць w с разрезом вдоль положительной полуоси. Если взять другую полосу (горизонтальную) шириной 2<Imz<4, тогда она так сама отобр. на всю пл.w с разрезом вдольположительной полуоси.

Показательная функция комплексной переменной.

Как известно, при x действительном e^x=lim_n(1+x/n)ⁿ.

Аналогично определяем e^zexpz= lim_n(1+z/n)ⁿ

Если z=x+iy- комплексное.

Можно показать, что |e^z|=| lim_n(1+z/n)ⁿ |=e^x, (Аrge^z)=

= (Аrg lim_n(1+z/n)ⁿ)=y.

Таким образом, комплексная показательная функция с комплексным показателем определяется равенством e^zexpz=e^x(cosy+isiny), так как lim_n(1+z/n)ⁿ= e^x(cosy+isiny)

Свойства показательной функции.

1. область определения - множество комплексных чисел. Это следует из того, что действительная функция =e^x определена при любом действительном x, а действительные функции sin и cos определены при  действительном y, а поэтому формула (4.7) имет смысл при  комплексном z=x+iy.

2. |e^z|=e^x; (Аrge^z)=y.

3. E(z^z)=C\{0}. Показательная функция не принимает нулевого значения, т. к. |e^z|=e^x0. Покажем, что показательная функция примет значение  комплексного числа 0, т. е. покажем, что уравнение e^z разрешимо относительно z=x+iy при 0. Представим в тригонометрической форме: =||(cos+isin),

Где - одно из значений Аrg, например, пусть =аrg - главное значение Аrg. Тогда уравнение примет вид: ||(cos+isin)=e^x(cosy+isiny)

Отсюда||=e^x, y-=2k, k=0, +-1, +-2,…;

X=ln||, y=+2k=arg+2k,

Итак, мы нашли решение уравнения

Z=x+iy=ln||+i(arg+2k), k=0,+-1,+-2,…

при  0

4. e^z1+z2=e^z1*e^z2 Пусть z₁=x₁+iy₁, z₂=x₂+iy₂ тогда

e^z1+z2=e^{(x1+x2)+i(y1+y2)}=e^x1+x2[cos(y₁+y₂)+isin(y₁+y₂)]

С другой стороны

e^z1*e^z2=e^x1(cosy₁+isiny₁)*e^x2(cosy₂+isiny₂)=e^x1+x2[(cosy₁cosy₂-siny₂siny₁)+i(siny₁cosy₂+siny₂ сosy₁)]=e^x1+x2[cos(y₁+y₂)+isin(y₁+y₂)] Получаем доказываемое уравнение

e^z1+z2=e^z1*e^z2

5. показательная функция аналитична во всей комплексной плоскости и (e^z)'=e^z .

Из определения показательной функции имеем: . Следовательно,

частные производные непрерывны в каждой точке z=x+iyС, так как дляx и y непрерывны функции e^x, cosy, siny. В  точке комплексной плоскости выполняются условия Коши-Римана:

Выполнение этих условий и непрерывность частных производных во всей комплексной плоскости означает аналитичность показательной функции во всей комплексной плоскости. Для нахождения производной используют формулу:

6. Показательная функция непрерывна во всей комплексной плоскости. Непрерывность следует из аналитичности функции. (функция аналитическая во всей комплексной плоскости дифференцируема в каждой точке плоскости, а из дифференцируемости всегда следует непрерывность функции).

7. показательная функция периодична с периодом равным 2i.

В самом деле