25. Паняцце кубавальнасці і аб’ёмау целау

Паняцце кубавальнасці

Азн. Мнагагр-м ( ) наз. цела, якое атр-ца аб^/яд-м трохвугольных пирамид, якия не маюць агульных пунктау.

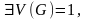У курсе геам-и разгл-ца: ф-цыя V, якая адлюстр-е мн-ва мнагагр-ау G у мн-ва сапр-х ликау: , такая, што мае улас-ци: 1) - неадмоунасць; 2) - адытыунасць; 3) яки наз-ца адзинкавым кубам - нармаванасць; 4) А=В => V(A)=V(B) - инварыянтнасць; 5) - манатоннасць.

Азн. Значэнне ф-цыи V, якое адпав-е мнагагр-ку G наз-ца аб^/ёмам мнагагр-ка.

Няхай . Разгл-м мн-кі умежаваны ў G ( )-(1^/) и мн-нік акрэсліны вакол G ( )-(2^/). Відавочна выконваецца няроўнасць: V(А)≤V(G) (1), и (2). З (1) вынікае, што мн-ва аб^/ёмау V(А) абмежавана зверху,а V(В) – знізу.

Т.ч sup{V(А)}=V_*(G) (3) – ніжні аб’ём фігуры G.

inf{V(В)}=V^*( G) (4)- верхні аб’ём фігуры G.

На падставе улас-цей даклад-й верх-й и нижн-й межау => V(А)≤ V_*(G) (3)

V^*( G) (4).

З (1), (2), (3) и (4) => V(А)≤ V_*(G) ≤ V^*( G) ≤ V(В) (5). З (5) => V_*(G) ≤ V^*( G).

Азн. V_*(G) наз-ца унутраным аб^/ёмам цела G, а V^*( G) – вонкавы (знешни).

Азн. Калі вык-ца роунасць V_*(G)=V^*(G)=V(G) (6), то цела G называецца кубавальным, а V(G) назваецца яго аб’ёмам.

Заувага: Калі цела G не змяшчае ниводнага мнагагр-ка, то унутраны V_*(G)=0.

Прыклады кубав-х фигур: 1) мн-к , т.як. вык-ца V_*(G)=V^*(G)=V(G) (6). 2)Куб, цыл-др;

Неабходныя и дастатковыя умовы кубавальнасци целау:

Тэарэма1: Для таго, каб цела G было куб-ным, н. и. д., каб яго мяжа Г(G) была целам нулявога аб^/ёму.

Тэарэма2: (на мове мнагагр-ау). Для таго, каб цела G было куб-ным, н. и. д., каб иснавали 2 пасл-ци мнаг-ау (А_n) i (B_n) адпаведна, якия змяшч-ца и змяшчаюць цела G (А_n) G, (B_n) G так, што = =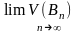V(G) (7).

Тэарэма3: (на мове куб-х целау). Для таго, каб цела G было куб-ным, н. и. д., каб иснавали 2 пасл-ци куб-х целау (А_n) i (B_n) адпаведна, якия змяшч-ца и змяшчаюць цела G так, што = = V(G) (8).

Паняцце аб’ёмау целау

1) Аб’ём прамога цылиндра

Азн. 1: Цылиндрычнай паверхняй наз-ца паверхня, якая утв-ца рухам прамой (утваральнай) // дадзенай прамой уздоуж крывой (кироунай).

Азн. 2: Прамым цылиндрам наз-ца цела, якое абмеж-на цыл-й паверхняй, утвар-я якога пл-ци, 2-мя пл-ми, якия // и перпенд-я гэтай утвар-й.

Азн. 3: Частки плоскасцей, якия утвар-ца выразаннем гэтых пл-цей //-ных пл-цям цылиндрычнай паверхни, наз-ца асновами цылиндра.

Тэарэма 1: Прамы цылиндр, у якога асновы квадравал-й фигуры Р з^/яул-ца кубав-м целам и падличваецца так: .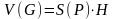

Выличэнне аб’ёма С-цела

Р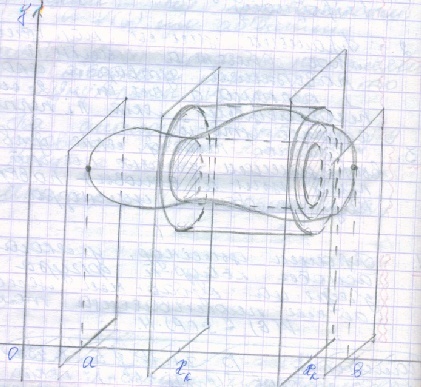 азгледзем цела G, якое заключана п/ж 2-мя //-ми пл-ми х = а, х = в, перп-ми воси Ох, такое, што: 1) у сечыве гэтага цела пл-ми, якия прах-ць праз любы п. воси Ох, ёй, атр-ца квадр-ыя фигуры (G: ), плошчы яких S(P)=S(x); 2) Ф-я S(x) – непар. на [a;b]; 3) Дзве праекцыи цела G на пл-ци Ох змяшчаецца адна у адну. Адзначанае цела наз-ца С-целам.

Тэарэма 2: С-цела – кубавальнае цела и аб’ём яго роуны: .

□ Разаб^/ём адрэзак [a;b]: Т-разбиука: а=х₀< х₁<…<x_k-1<x_n=b; и праз кожны пункт разбиуки правядзем пл-ци Ох. Атрымаем n-слаёу. Ф-цыя S(x) па азн-ню непар-я на [a;b] и на кожным з частковых адр-у [х_к-1; х_к] i на гэтых адр-ках яна будзе прымаць найм-е и найб-е знач-ни. Пабудуем прамыя цыл-дры, заключ-я п/ж пл-цями х = х_к-1, х = х_к , якия маюць адпаведны аб’ём. m_k , M_k (найм-я и найб-я плошчы), m_k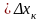 , M_{k .} Т.ч. атр-ся 2 пасл-ци цыл-ных целау, якия , => , .

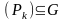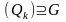(1) (2) V(P_n) – аб’ём прыступ-га цела, якое змяшч-ца у целе S=S; V(Q_n) - аб’ём прыступ-га цела, якое змяшч-е цела S=S. На падставе т.3. абодва прыступ-я целы з^/яул-ца кубавал-ми целами. Т.ч. мы пабудавали 2 пасл-ци куб-х целау (P_n) и (Q_n), якия на падставе т.3. задав-е умове: = =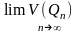 V(G) (3). З др. боку сумы (1) и (2) з^/яул-ца интэгр-ми и таму яны маюць адзины лимит: = = (4). Параунаем правыя частки (3) и (4) и => => (5). ■

Заувага: Для знах-ня аб’ёма цела па фор-ле (5) даст-ва мець фор-лу плошчы папярэчнага сечыва.

Прыклад: 1)Знайсци аб’ём пирамиды. Або дак-ць, што аб’ём пирамиды роуны: . 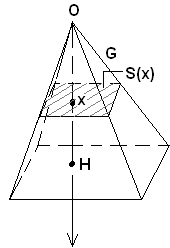Р – квадрав-я фигура. Па т. 2: (5*). Цела G з^/яул-ца кубав-м. Кавальеры даказау, што парал-я асновы падоб-х пирамид аднос-ца як квадраты их вышынь:

2) Выкарыстанне формулы для вылічэння аб’ёму шара.

x²+y²=a²; y²=a²–x²; 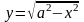; ; V(δ)= .