5. Над і нак двух лікаў
Азн.
Нях.
.
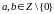Агульным дзельнікам лікаў a
і
b
наз. такі цэлы лік, які дзеліць a
і
b.
Абазн.
.
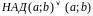Азн. Найб.АД лікаў a і b наз. такі іх агульны дзельнік, які дзеліцца на любы іх агульны дзельнік.
Пр. 1 НАД(2,-4)=2, НАД(2,-4)=-2.
Азн. Нях. . Агульным кратным наз лік, які падзяляецца без астачы на a і b.
Азн.
Найм АК
a
і
b
наз
такі натуральны лік
с,
які: 1) с – агул крат, 2)
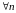агул крат
.
Абазн
.
Т.
.
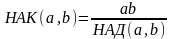НАД – выкар-цца пры скарочальнасці дробаў, НАК – пры складанні дробаў.
Алгарытм Эўкліда
Працэс.
Нях.
.
Падзелім
a
на
b
з астачай:
(1)
Тады
b
дзеліцца на
з астачай:
(2)
дзеліцца
на
:
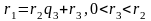(3)
............................
дзеліцца
на
:
(n)
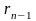дзеліцца
на
:
(n+1)
Т.
як
,
дзе ўсе лікі нат-ыя, то працэс дзялення
не м. б. бясконцым.
Т.
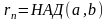□ Пакажым, што
.
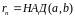З роўнасці (n+1) вынікае, што дзеліцца на
(n)
...........................................................
(2) b
(1) a .
,
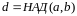
З
(1)
дзеліцца на d
(2) дзеліцца на d
...................................
(n) дзеліцца на d ■
6. Поле кампл. Лікаў. Геаметр. Прадстаўленне кампл. Лiкаў
Азн.
Кампл. лiкам
будзем
наз. упарадкаваную пару (a;
b),
дзе
Мн-ва кампл. лiкау будзем абазн. С
Азн.Сумай
кампл.
лiкау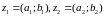
наз.
кампл. лiк
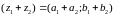
Азн.
Здабыткам
кампл. лiкау
наз. кампл.
лiк
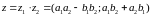
Тэар. Мноства кампл. лiкау з аперацыямi складання i здабытку з-ца полем
Тэар.
У мн-ве кампл. лікаў
С разгл. падмноства
.
Мы м. атаесамляць (
)
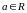з
кампл. лікам (а;0); інакш м.
мн-ва R
лікаў з мн-вам кампл. лікаў.
,
Доказ:
(складання)
і
=>
,
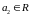які
з кампл. лікам
.
Складаем кампл. лікі, якія
з R
лікамі
.
.
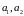Азн. Уяунай адзiнкай будзем наз. кампл. лiк i=(0;1)
Ул.
Доказ:
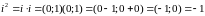
Ул. z =(a,b) => z =a+bi Доказ: a+bi=(a;0)+(b;0)(0;1)=(a;0)+(0;b)=(a;b)=z
Азн.
Выяуленне
кампл.
лiка
z =(a,b) у
выглядзе
z =a+bi наз
алгебраiчнай
формай
кампл.
лiка.
– сапраўдная частка,
– уяўная частка.
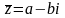– лік,
спалучаны
да
.
– модуль
к. ліку.
Аргументам
кампл. ліку z
наз. вугал паміж восю R
лікаў і вект.
,
які адпавядае Z.
(
).
Г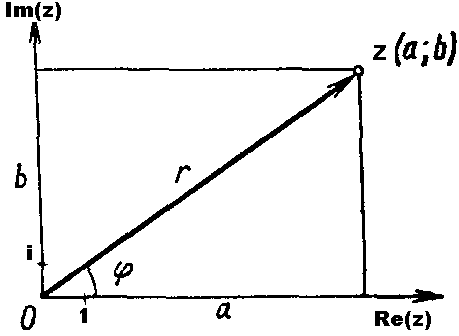
еам.
інтэрпр. кампл. ліку
Няхай
z
=a+bi
. Разгл. пл-ць і на пл-ці пункт Z(а,
b).
Маем біектыўнае адлюстраванне паміж
кампл. лікамі z
і п-мі пл-ці Z
і вектарамі
.
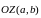Пункт Z
і
-
геам. інтэрпрэтацыя кампл. ліка z
Т.
аб модулі сумы і рознасці к. лікаў.1)
,
2)
.
□
,
,
,
,
.
.
.
,
.
■
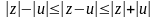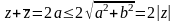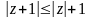Тэар.
Калі
,
то
(1) Доказ:
,
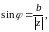
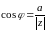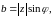
Азн. Выяўленне кампл. ліка у выглядзе (1) наз. трыганаметр. формай кампл. ліку z.
Т.
аб падвышэнні ў ступень.
Модуль здабытку 2-х кампл. лікаў роўны
здабытку іх модуляў, а аргумент здабытку
роўны суме аргументаў гэтых кампл.
лікаў. □ Нях.
,
.
.
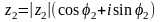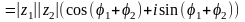■ Гэту т-у м. абагульніць на любы лік
сумножнікаў. Тады
,
.
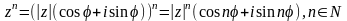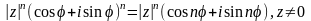– формула
Муаўра.
Т.
аб здабыванні кораня з кампл. ліку.
Калі кампл. лік а
=> існуе роўна n
розных каранёў n-ай
ступені з а.
=>
,
,
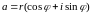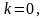
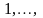
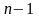дзе
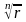–арыфметычны
корань n-й
ступені з дадатнага рэчаіснага ліку
,
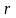