Азначэнні камплексных функцый камплекснай зменнай

Аз: калі кожнаму zD пастаўлены у адпавелнасць лік , з мноства E,то какжуць што адзначана функцыя =f(z). D- абсяг існавання функцыі, E-мноства значэнняў функцыі, z- незалежная комплексная зменная=>камплексныя функцыі=>z- камплексная, і - камплексная.

z=x+iy→=u+iv., u=u(x,y), v=v(x,y)

f(z)= u(x,y)+iv(x,y)

Аз: sinz=(e^iz-e^-iz)/2i

Аз: cоsz=(e^iz+e^-iz)/2

Т: Каб функцыя =f(z) была непарыўнай у пункце z₀=x₀+iy₀ неабходна і дастаткова каб непарыўнымі былі яе рэчаісная(u)і уяўная(v) часткі у пункце(x₀,y₀)

Свойства:

1. sinz и cosz определены для всех z С, так как zС определена показательная функция e^z.

2. Функции непрерывны во сей комплексной плоскости, так как непрерывна во всей комплексной плоскости функция w=e^z.

3. Функции являются переодическими с периодом 2. Действительно, имеем

4. функции являются аналитическими .

5. например для функции w=sinz. Выделим действительную и мнимую части функции.

6. 

7. Отсюда имеем, что

8. 

9. Легко проверить, что условие Коши-Римана

10. 

11. выполняется для всех zС. Так как функции u(x,y) и v(x,y) имеют непрерывные частные производные и условие К-Р выполняются для всех zС, то ф. w=sinz является аналитической во всей комплексной плоскости.

12. Вычислим производную функции w=sinz.

13. 

14. Аналогичным образом доказывается, что (cosz)’=-sinz.

15. Разложение y=sinz в ряд:

16. 

8. Лагарыфмічная функцыя і яе асноўныя ўласцівасці. Раскладанне у ступеневы шэраг

(1) -лікавая паслядоунасць.

(2) - частковыя суммы

Пару, якая складзена з паслядоунасцей (1) и (2) (3) наз лікавым шэрагам.

Шэраг віду , дзе C_n, a - ступеневы шэраг.

Тэарэма: Калі на інтэрвале (a-R;a+R) функцыя f(x) раскладаецца у ступеневы шэраг, то гэта раскладанне адзінае і мае выгляд:

-шэраг Тэйлора

- шэраг Макларэна

Формула Тэйлора: , дзе - астача шэрагу.

- астача шэрага (1) пасля n-га складніка, ,

Разгледзім дзве формы астачы:

1) астача у форме Кашы: -лік, модуль якога <1.

2) астача у форме Лагранжа:

Калі функцыя y=a^x (0<a, a1) страга манатонна і непарыуна, тады згодна тэарэме аб адваротнай функцыі для гэтай фукцыі існуе і непарыўна адваротная функцыя

x=f ^­-1(y). гэта адваротная функцыя таксама манатонна і непарыўна.

Аз: y=f^-1(x)- адваротная да паказчыкавай функцыі у=а^х наз. лагарыфмічнай функцыяй пры аснове a.

Роўнасць x=f ^-1(y) азначае , што  ліку b>0, b належыць D_f^-1, функцыі f ^-1 ставіцца у адпаведнасць лік x₀Е_f^-1 такі, што a^x₀=b. Значэнне x₀ лагарыфмічнай функцыі якое адпавядае b роунае паказчыку ступені, у якую трэба узвесці лік a , каб атрымаць лік b. Такі паказчык наз. лагарыфмам b па аснове a.

Вызначым усе гэта формулай y=log_ax. Гэта функцыя валодае наступнамі уласцівасцямі:

1. D_y=(0;), Е_y=(-;+)

2. Функцыя нарастальная калі а>1, спадальная калі 0<a<1.

3. функцыя непарыуная у D_y

4. log_a1=0

5. Калі a>1:log_ax<0, калі x<1; log_ax>0, калі x>1

6. Калі 0<a<1:log_ax<0, калі x>1; log_ax>0, калі x<1

7. Калі a>1 lim_x+log_ax=+, lim_x0+0log_ax=-

8. Калі 0<a<1 lim_x+0log_ax=+, lim_x+log_ax=

Дыферынцавальнасць:

Доказ:

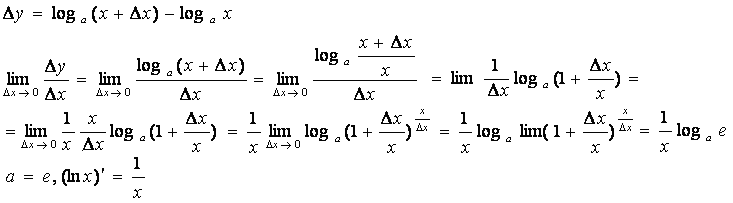
Раскладанне функцыі ln у шэраг

f(x)=ln(1+x): f(x)=1/(1+x), f’(0)=1, f(x)=(-1)1/(1+x)², f’’(0)=-1, f(x)=2!/(1+x)³, f’’’(0)=2!, ..., f⁽ⁿ⁾(x)=(-1)^n-1(n-1)!/(1+x)ⁿ, f⁽ⁿ⁾(0)=(-1)^n-1(n-1)!

Ln(1+x)=x - x²/2 + x³/3 - x⁴/4 +...+ (-1)ⁿ⁺¹xⁿ/n+…= +R_n.

Ln(1-x)= -x - x²/2 - x³/3 - x⁴/4-...- xⁿ/n-…=

Шэраг збягаецца на (-1;1), і калі x=1 (ln0=1) шэраг збягаецца, калі x=-1 (ln1=0) шэраг гарманічны, які разбягаецца, адсюль вынікае , што абсяг збежнасці шэрага (-1; 1].

Даследуем шэраг з дапамогай астачы, паказвая што яна →0. Калі x[0;1] будзем выкарыстоўваць астачу шэрага ў форме Лагранжа: R_n(a)=f⁽ⁿ⁺¹⁾(c)(x-a)ⁿ⁺¹/(n+1)!

R_n(a,x)=(-1)ⁿn!(x-a)ⁿ⁺¹/[(1+ c)ⁿ⁺¹(n+1)!].

Паложым a=0,R_n(0,x)=xⁿ⁺¹/[(1+c)ⁿ⁺¹n+1)!]≤1/n+1, адсюль выникае, што для x([0;1],Rn→0 на дадзеным адрэзку шэраг збягаецца да функцыі f(x).

Калі x((-1;0) астачу ацэньваем у форме Кашы. Маем (Rn(x)(=(-1)ⁿ xⁿ⁺¹(1-θ)ⁿ/(1+ θx)ⁿ⁺¹, 0< θ<1, так што

R_n(x)≤{xⁿ⁺¹/1-x}*(1-θ)/(1+ θx)ⁿ ;{1-x<1+1+ θx , x>θx , так як x<θx }, так як x>-1 будзе 1+ θx>1- θ, тады паслядоўнасць множ. меньш за 1, => толькі x<1, заведама R_n(x)→0

Астача на интэрвале (-1;1) →0 кали n→ , г.зн. што формулы раскладання можна выкарыстовываць для набліжанага вылічэння значэнняу функцыи Ln(1+x).