2. Неабходная і дастатковая прыкмета збежнасці паслядоунасці

Ф-я f наз лікавай, калі D(f) – мноства лікаў і E(f) – мноства лікаў.

Лікавай паслядоунасцю наз лікавая функцыя, якая вызначана на мностве натуральных лікаў, абазн {Xn}.(n=1,2,3,…)

Лік а наз лімітам паслядоунасці {Xn} калі , калі для любога ε>0 існуе такі нумар , што для нумароу n> выконваецца няр-ць , . Лік а наз лімітам паслядоунасці {Xn} калі , калі ў любым ε-наваколлі змешчаны амаль усе члены дадзенай паслядоўнасці пачынаючы з некаторага нумара .

Прыклад: т/д: .

Калі паслядоўнасць мае ліміт, то яна збежная.(збежная паслядоўнасць – абмежаваная).

АЗН. Лiкавая паслядоунасць (а_n) наз. збежнай да лiку а, калi такi што для выконваецца няроунасць , дзе М – сталы лiк.

Збежная паслядоунасць можа мець толькi адзiн лiмiт.

Прыклады: пры n→ – п-ць збежная, пры n→ – п-ць разбежная.

АЗН: Лікавая пасл-ць (а_n) наз-ца фундаментальнай у сэнсе Кашы, калі існуе рэчаісны лік , такi што для выконваецца няроунасць .

Тэарэма Кашы: Каб пасл-ць (а_n) была збежнай неабходна і дастаткова, каб яна была фундаментальнай у сэнсе Кашы.

Доказ (неабходнасць): дано, што lim a_n=а пры n→ (а_n-а) ёсць Бясконца Малая Паслядоунасць (limXn=0 пры n→ ). Існуе , такi што для і Калі скласці гэтыя няроўнасці для .

(Дастатковасць): Г. зн. для . Зафіксуем , а n=m+p, дзе . Тады ўмова фундаментальнасці , г.зн. пасл-ць будзе абмежаванай. Паколькі 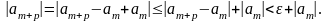сярод лікаў 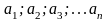ёсць самы большы і самы меньшы, значыць і пасл-ць (а_n) будзе абмежаванай зверху і знізу. Па тэарэме Бальцана-Вейерштраса з яе можна вылучыць збежную падпасл-ць , , пры k→ . 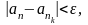калі . пры k→ пры k→

3. Ліміт лікавай паслядоунасці. Тэарэма Бальцана-Вейерштрасса

Ф-я f наз лікавай, калі D(f) – мноства лікаў і E(f) – мноства лікаў.

Лікавай паслядоунасцю наз лікавая функцыя, якая вызначана на мностве натуральных лікаў, абазн {Xn}.(n=1,2,3,…)

Лік а наз лімітам паслядоунасці {Xn} калі , калі для любога ε>0 існуе такі нумар

, што для нумароу n> выконваецца няр-ць , .

Лік а наз лімітам паслядоунасці {Xn} калі , калі ў любым ε-наваколлі змешчаны амаль усе члены дадзенай паслядоўнасці пачынаючы з некаторага нумара

Прыклад: т/д: .

Калі паслядоўнасць мае ліміт, то яна збежная.(збежная паслядоунасць – абмежаваная).

Пункт Xo наз лімітавым пунктам лікавага мн-ва X, калі у любым наваколлі пункта Xo утрымліваецца бясконцае мн-ва пунктаў з X.

Калi выконваецца няроунасць , то лiкав. пасл-ць наз. абмежаванай.

Прынцып Бальцана-Вейерштраса: усякае абмежаванае лікавае мн-ва мае хаця б адзін лімітавы пункт.

Доказ:

1) Т.як мноства Х абмежавана, то існуе адрэзак [a,b], які утрымлівае гэта мноства Х.

2) Няхай даужыня гэтага адрэзка =d, (b-a=d).

3) Раздзелім адрэзак [a,b] папалам і выбярэм ту яго палову даужыні , якая утрымлівае бясконцае мн-ва элементаў з Х.

4) Раздзелім адрэзак папалам и выдзелім ту яго палову даужыні , якая утрымлівае бясконцае мн-ва элементаў Х.

5) Прадаўжаючы гэты працэс бясконца, выдзелім адрэзак даужыні 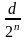. Атрымаем паслядоўнасць укладзеных адрэзкау { }, . .

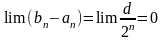6) Пакажам, што с- лімітавы пункт для мн-ва Х. Выбярэм адвольнае дэльта наваколле пункта с: . Т.як 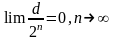, то пачынаючы з нейкага пункта 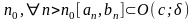. Г.зн. што у утрым-ца бясконцае мн-ва элементаў мноства Х. Г.зн. што с-лімітавы пункт мн-ва Х.

Разгледзiм пасл-ць 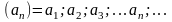Няхай адвольная нарастальная пасл-ць. У такiм разе адпаведная пасл-ць 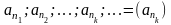наз-ца падпаслядоунасцю у дачыненнi да першапачатковай пасл-цi (а_n).

Тэарэма: Калi (а_n) збежная пасл-ць i lim a_n = а пры n→ , то кожная яе падпасл-ць будзе збежнай да таго самага лiмiту , пры k→ .

Тэарэма аб укладзеных адрэзках: Калi [a₁; b₁]>[a₂; b₂]>…>[a_n; b_n]>… i пры n→ , то iснуе агульны лiмiт , пры n→ .

Тэарэма Бальцана-Вейерштраса. З кожнай абмежаванай пасл-цi (с_n) можна вылучыць збежную падпаслядоўнасць.

Доказ. З нягодай абмежаванасцi усе элементы пасл-цi належаць адрэзку [a₁; b₁]. Дзелiм гэты адр-к папалам i з двух атрыманых адрэзкау выбiраем той, якому належыць бясконцае мноства значэнняу пасл-цi (элементау). Абазначым яго [a₂; b₂]. Адр-к [a₂; b₂] зноу дзелiм папалам. Абазначым [a₃; b₃] той адр-к, на якiм будзе вялiкае мноства пасл-цi (с_n). Гэты працэс працягваецца да бясконцасцi. У вынiку мы атрымаем [a₁; b₁]>[a₂; b₂]>…>[a_n; b_n]>…, пры чым , пры n→ . Па тэарэме аб укладзеных адрэзках , пры n→ . Возьмем любы элемент , на другiм кроку – , на трэцiм – i г.д., на к-ым кроку – i г.д. У вынiку мы атрымаем пасл-ць , для элементау якой выконваецца няроунасць пры k→ .

Заувага. Калi пасл-ць будзе неабмежавана зверху, то з яе можна вылучыць падпасл-ць збежную да "+"бясконцасцi.