Алгебра

1. Бінарныя дачыненні. Дачыненне эквівалентнасці і падзел на класы.

2. Кольца. Прыклады кольцаў. Найпрасцейшыя уласцівасці кольца.

Падкольца. Гомамарфізмы і ізамарфізмы кольцаў.

3. Сістэма натуральных лікаў.

4. Кольца цэлых лікаў. Тэарэма аб дзяленні з астачай.

5. Найбольшы агульны дзельнік і найменшы агульны кратны двух лікаў.

6. Поле камплексных лікаў. Геаметрычнае выяўленне камплекснага ліку.

7. Рауназначныя сістэмы лінейных раўнанняў. Рашэнне сістэмы

ліненных раўнанняў метадам паслядоўнага выключення

невядомых. Крытэрыі супольнасци сістэмы лінейных раўнанняў.

8. Ізамарфізм вектарных прастораў. Бaзіс і памернасць канечнамернай

вектарнай прасторы. Падпрасторы.

9. Простыя лікі. Бясконцасць мноства простых лікаў. Кананічны расклад

састаўнога ліку і яго адзінасць.

10. Асноўныя ўласцівасці параўнанняў. Прыкметы падзельнасці. Тэарэма

Эйлера i Ферма.

11. Параўнанні з невядомымі. Лінейныя параўнанні.

12. Пераўтварэнне простага дробу ў дзесятковы і вызначэнне даўжыні

перыяду дзесятковага дробу.

13. Паліномы над полем. Найбольшы агульны дзельнік двух паліномаў і

алгарытм Эўкліда. Раскладанне палінома ў здабытак непрыводных множнікаў i яго адзінасць.

14. Непрыводныя паліномы над полем камплексных i сапраўдных лікаў.

15. Простае алгабраічнае пашырэнне поля. Вызваленне ад алгебраічнай

ірацыянальнасці ў назоўніку дробу.

1. Бінарныя дачыненні. Дачыненне эквівалентнасці і падзел на класы

Азн. Няхай А і В . уласцівасць ρ (a, b), і , тады кажуць, што зададзена бінарнае дачыненне паміж мноствамі А і В.

Пр. a/ b – цотны лік,

Абсяг вызн. і абсяг знач. = АхВ.

Далей будзем разглядаць бін дач на мн-ве А ( )

Азн.: 1. a ρ a, - рэфлексіўнасць.(a a)

2. , - антырэфлексіўнасць. (a>a)

3. a ρ b, то b ρ a , - сіметрычнасць.(a, b – цот)

4. , - антысіметрычнасць.

5. a ρ b і b ρ a, то a=b, - асіметрычнасць.( a b і b a, то a=b)

6. a ρ b і b ρ c, то a ρ c, - транзітыўнасць.(a>b, b>c, то a>c)

Азн. Дачыненне ρ - дачыненне эквівалентнасці, калі яно рэфлексіўнае, сіметрычнае, транзітыўнае. Абазн .

Напр. =,||, раўназначнасць, падабенства.

Азн. Няхай на мностве Х зададзена дачыненне эквівал ρ мн-ва усіх элементау мн-ва Х, якія эквівалентны элем х, наз классам эквівалентнасці х (адносна дачынення ρ) і абазн , , .

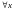
Сцв. 1. 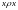(рэфлекс.)

2.

3.

Д-з 3: 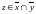, ( транзітыунасць)

транзіт .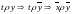

Аналаг

Азн. Калі зададзена не пустое мн-ва Х і с-ма яго падмн-вау , дзе , і такіх, што і тады, калі 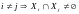, тады кажуць, што зедадзена разбіцце мн-ва Х.

Т. З кожнай эквівалентнасцю ρ на А звязана разбіцце мноства А на класы і гэтымі класамі будуць усе розныя класы ρ-эквівалентеасці.

Д-з. Адносіна ρ на А валодае ўласцівасцямі рэфлексіўнасці, сіметрычнасці, транзітыўнасці.

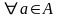маем а ρ а, зн. ,

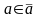Калі 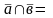Ø, то .

Дап. што , тады і , г.зн. с ρ а і с ρ в - сіметр. Т.я. ρ - сіметр. і транзітыўна, то атр-ца а ρ с і с ρ в →а ρ в.

Няхай і а ρ в →х ρ в, таму . Т.ч. 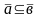. Аналагічна паказваецца і адваротнае , зн. .

З даказанага вынікае, што калі Ø. Т.ч. робім выснову: усе розныя класы ρ-эквівалентнасці 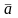ствараюць разбіцце мноства А.