
- •Апаратні та програмні засоби пеом.
- •Постановка основних граничних задач для рівнянь у частинних похідних другого порядку.
- •Лінійна задача оптимальної швидкодії (на прикладі системи керування, що описується системою двох диференціальних рівнянь першого порядку, із застосуванням принципу максимуму Понтрягіна).
- •Принцип оптимальності Белмана. Рівняння Белмана для задачі з дискретним часом. Схема методу динамічного програмування.
- •Частинний коефіцієнт кореляції. Властивості та методика використання.
- •Реляційна модель Кодда. Реляційна алгебра.
- •Банахові простори. Лінійні оператори та лінійні функціонали у банахових просторах.
- •Норма функціонала - .
- •Теорема Хана-Банаха про поширення лінійного функціоналу.
- •Інтегральні рівняння. Теореми Фредгольма.
- •Вивід у граматиці. Дерево виводу. Лівостороння та правостороння стратегії виводу
- •Математичні моделі довготривалого страхування.
- •Метод функції Гріна розв’язку граничних задач.
- •Міра Лебега та її властивості.
- •Метод теорії потенціалу.
- •Проблеми моделювання динамічних систем з розподіленими параметрами.
- •Інтегральні лишки. Лема Жордана.
- •Класифікація запитів.
- •Метод Фур’є розділення змінних (на прикладі рівнянь гіперболічного типу).
- •Метричні простори. Приклади. Повні метричні простори. Принцип стискуючих відображень.
- •Комплексна площина. Сфера Рімана.
- •Степеневі ряди. Теореми Абеля.
- •Принцип максимуму Понтрягіна. Теорема про необхідну умову оптимальності (закріплені кінці, закріплений час, без доведення).
- •Ермітові оператори, проектори. Спектральний розклад ермітових операторів.
- •Поняття мовного процесора. Типи мовних процесорів. Основні фази мовного процесора.
- •Структура мовного процесора типу транслятор
- •Структура мовного процесора типу інтерпритатор
- •Гільбертові простори. Нерівність Коші-Буняковського. Визначення норми.
- •Керованість для нестаціонарних та стаціонарних лінійних систем. Необхідні та достатні умови цілком керованості.
- •Означення (цілком керован на пром)
- •Скінченні автомати. Методика побудови лексичного аналізатора на основі скінченного автомата.
- •Зауваження 1 (узагальнен Означення 1)Задачу знаходження вектору - стану системи (1) або окремих його компонент за відомою на деякому проміжку функцією (3),
- •Регулярні множини та регулярні вирази, їх звязок із скінченними автоматами. Основні тотожності в алгебрі регулярних виразів.
- •Деяка мова задається скінченим автоматом коли мова є регулярною множиною.
Метод теорії потенціалу.
Визначення основних теплових потенціалів.

Теорема про граничні значення теплового потенціалу подвійного шару.
Теорема.
Нехай S
замкнена поверхня Ляпунова,
![]() неперервна на
неперервна на
![]() щільність. Тоді тепловий потенціал
подвійного шару має на поверхні S
неперервні граничні значення при підході
до будь-якої точки
щільність. Тоді тепловий потенціал
подвійного шару має на поверхні S
неперервні граничні значення при підході
до будь-якої точки
![]() зсередини та ззовні, і ці граничні
значення мають вигляд:
зсередини та ззовні, і ці граничні
значення мають вигляд:

Теорема про граничні значення нормальної похідної теплового потенціалу простого шару.
Теорема.
Нехай S
замкнена поверхня Ляпунова,
![]() неперервна на
щільність. Тоді при підході до поверхні
S
вздовж нормалі для будь-якого фіксованого
значення часу t0
потенціал простого шару має неперервні
граничні значення нормальної похідної
при підході зсередини та ззовні, і ці
граничні значення обчислюються за
формулами:
неперервна на
щільність. Тоді при підході до поверхні
S
вздовж нормалі для будь-якого фіксованого
значення часу t0
потенціал простого шару має неперервні
граничні значення нормальної похідної
при підході зсередини та ззовні, і ці
граничні значення обчислюються за
формулами:

Проблеми моделювання динамічних систем з розподіленими параметрами.
СРП-система,
функція стану y(x,t)
в просторово-часовій обласвті
![]()
задовольняє
рівнянню:
![]() -
диференціальна
модель. (1),
-
диференціальна
модель. (1),
де
![]() ,
,
![]() – задані
матричні оператори,
– задані
матричні оператори,
![]() -
зовнішнє динамі збурення на систему.
-
зовнішнє динамі збурення на систему.
Початково крайові умови :
![]() ,
,
![]() ; (2)
; (2)
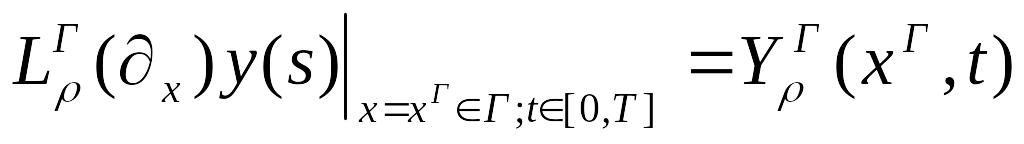 ,
,
![]() . (3)
. (3)
Інколи моделюються спостереження
![]() ,
,![]() (4)
(4)
Знаходження y(x,t) є прямою задачею, обернені задачі – задачі керування та спостереження за системою.
Інтегральна
модель.
Виражає залежність
![]() від
від
![]() в
явній формі :
в
явній формі :
 ,де
,де![]() відома
матрична ф-ція
Гріна. (5)
відома
матрична ф-ція
Гріна. (5)
Цю модель можна записати у вигляді:
![]() (6)
(6)
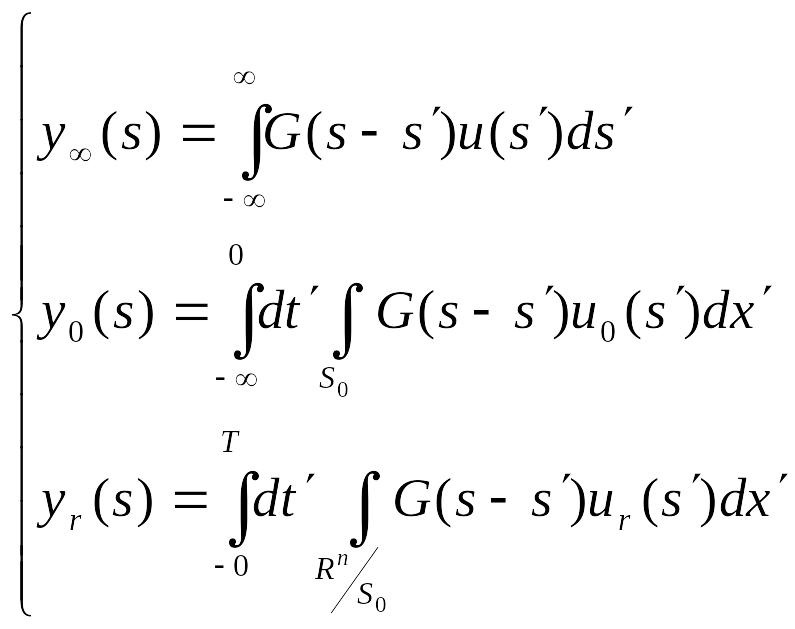 (7)
(7)
де
![]() і
і
![]() - фіктивні зовнішні динамічні збурення,
яких не існує, що діють за межами
розглядуваної
- фіктивні зовнішні динамічні збурення,
яких не існує, що діють за межами
розглядуваної
![]() якими моделюється ефект впливу на
систему поч.-кр. умов.
якими моделюється ефект впливу на
систему поч.-кр. умов.
Проблеми переходу від (1)-(3) до (6)-(7):
1)
Необх. побуд. функцію
![]() ;
;
2)
Знайти моделюючі функції
![]() та
та
![]() .
.
Проблеми
моделювання: іноді модель не повна ( не
узгоджено розмірність і порядок); не
адекватний опис динаміки системи. Інакше
: потрібно часто розв‘язувати задачі
типу
![]() ,
де
,
де
![]() -параметр.
-параметр.
Інтегральні лишки. Лема Жордана.
Інтегральним
лишком аналітичної функції
![]() в околі ізольованої особливої точки
однозначного характеру називається
коефіцієнт
в околі ізольованої особливої точки
однозначного характеру називається
коефіцієнт
![]() у розвиненні функції
в околі цієї точки в ряд Лорана. Позначають
інтегральний лишок так.
у розвиненні функції
в околі цієї точки в ряд Лорана. Позначають
інтегральний лишок так.![]() ,
де
,
де
![]() -
довільний гладкий замкнутий контур, що
містить всередині себе точку а
і малий настільки, що
аналітична скрізь всередині нього і на
ньому.
-
довільний гладкий замкнутий контур, що
містить всередині себе точку а
і малий настільки, що
аналітична скрізь всередині нього і на
ньому.
Лема
ЖорданаЯкщо
на послідовності концентричних півкіл
![]() функція
функція
![]() рівномірно відносно аргумента Z
прямує до нуля при
рівномірно відносно аргумента Z
прямує до нуля при
![]() ,
то для довільного
,
то для довільного
![]() має місце
має місце

![]() Покладемо
Покладемо
![]() ,
,
![]() .
Оцінимо величину на контурі
.
Оцінимо величину на контурі
![]()
![]() Виберемо
Виберемо
![]() таким,щоб
таким,щоб
![]() .
Врахуємо також те, що при
.
Врахуємо також те, що при
 .
Тоді
.
Тоді

при
осуільки
![]() ,
а величина
,
а величина
![]() обмежена
обмежена
![]()
Зауваження
1. Лема вірна
і у випадку якщо
![]()
Для доведення достатно довести що на ділянках II та III інтеграл прямує до нуля.
Зауваження
2. Якщо за
вхяти
![]() то при вимогах накладених на
лемож Жордана, в
то при вимогах накладених на
лемож Жордана, в
![]() ,
вірна рівність
,
вірна рівність
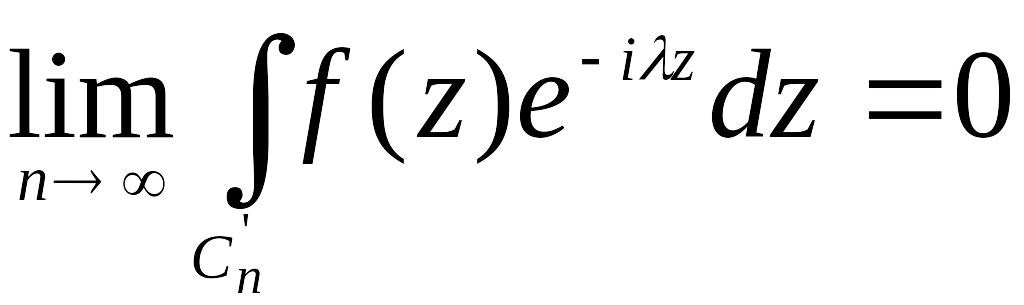
Зауваження 3. Нехай
![]()
задовольняє
умовам леми Жордана в
![]() маємо
маємо

Загальне поняття інтегрованої функції. Поняття про інтеграл Лебега.
Послідовність
простих інтегрованих функцій
![]() називається вимірною у середньому
, якщо
називається вимірною у середньому
, якщо
![]() виконується
виконується
![]() .
.
Нехай
маємо простір
![]() зі скінченною мірою. Визначена на ньому,
вимірна функція
зі скінченною мірою. Визначена на ньому,
вимірна функція
![]() називається інтегрованою,
якщо існує фундаментальна в середньому
послідовність простих інтегрованих
функцій
називається інтегрованою,
якщо існує фундаментальна в середньому
послідовність простих інтегрованих
функцій
![]() ,
що збігається за мірою до
,
при
,
що збігається за мірою до
,
при
![]() .
Інтеграл Лебега -
.
Інтеграл Лебега -
![]() .
.
Властивості
інтеграла (
![]() - прості вимірні функції ) :
- прості вимірні функції ) :
лінійність (
 ) ;
) ;
невід‘ємність (
 ;
;
![]() ;
;
монотонність (
 );
);
оцінка модуля інтеграла (
 );
);абсолютна неперервність (
 -абс.
непер ф-ія відносно
,
);
-абс.
непер ф-ія відносно
,
);зліченна адитивність (
 ,
,
 ,
,

 ).
).
