
- •Апаратні та програмні засоби пеом.
- •Постановка основних граничних задач для рівнянь у частинних похідних другого порядку.
- •Лінійна задача оптимальної швидкодії (на прикладі системи керування, що описується системою двох диференціальних рівнянь першого порядку, із застосуванням принципу максимуму Понтрягіна).
- •Принцип оптимальності Белмана. Рівняння Белмана для задачі з дискретним часом. Схема методу динамічного програмування.
- •Частинний коефіцієнт кореляції. Властивості та методика використання.
- •Реляційна модель Кодда. Реляційна алгебра.
- •Банахові простори. Лінійні оператори та лінійні функціонали у банахових просторах.
- •Норма функціонала - .
- •Теорема Хана-Банаха про поширення лінійного функціоналу.
- •Інтегральні рівняння. Теореми Фредгольма.
- •Вивід у граматиці. Дерево виводу. Лівостороння та правостороння стратегії виводу
- •Математичні моделі довготривалого страхування.
- •Метод функції Гріна розв’язку граничних задач.
- •Міра Лебега та її властивості.
- •Метод теорії потенціалу.
- •Проблеми моделювання динамічних систем з розподіленими параметрами.
- •Інтегральні лишки. Лема Жордана.
- •Класифікація запитів.
- •Метод Фур’є розділення змінних (на прикладі рівнянь гіперболічного типу).
- •Метричні простори. Приклади. Повні метричні простори. Принцип стискуючих відображень.
- •Комплексна площина. Сфера Рімана.
- •Степеневі ряди. Теореми Абеля.
- •Принцип максимуму Понтрягіна. Теорема про необхідну умову оптимальності (закріплені кінці, закріплений час, без доведення).
- •Ермітові оператори, проектори. Спектральний розклад ермітових операторів.
- •Поняття мовного процесора. Типи мовних процесорів. Основні фази мовного процесора.
- •Структура мовного процесора типу транслятор
- •Структура мовного процесора типу інтерпритатор
- •Гільбертові простори. Нерівність Коші-Буняковського. Визначення норми.
- •Керованість для нестаціонарних та стаціонарних лінійних систем. Необхідні та достатні умови цілком керованості.
- •Означення (цілком керован на пром)
- •Скінченні автомати. Методика побудови лексичного аналізатора на основі скінченного автомата.
- •Зауваження 1 (узагальнен Означення 1)Задачу знаходження вектору - стану системи (1) або окремих його компонент за відомою на деякому проміжку функцією (3),
- •Регулярні множини та регулярні вирази, їх звязок із скінченними автоматами. Основні тотожності в алгебрі регулярних виразів.
- •Деяка мова задається скінченим автоматом коли мова є регулярною множиною.
Вивід у граматиці. Дерево виводу. Лівостороння та правостороння стратегії виводу
Нехай G-граматика. Будемо казати, що послідовність v безпосередньо породжує послідовність w: v w, якщо v=xUy, w=xuy, та існує правило U ::= u
Будемо казати, що послідовність v породжує w: v+ w, якщо існує посліовність v=u0 u1 … un =w
Лівостороння стратегія виводу w в G - це така стратегія безпосереднього виводу де на кожному кроці береться перший з ліва направо нетермінал. Правостороння протилежна лівосторонній.
Синтаксичні дерева.
Синтаксичне дерево - дерево, корінь якого є аксіома, проміжні вершини позначені елементами з N, на кроні знаходяться елементи з множини E.

Контекстно-вільні
граматики:
Породжуюча
граматика (за Хомським): G=<N,E,P,S>, де N
- допоміжний алфавіт (алфавіт нетерміналів);
E - основний алфавіт (алфавіт терміналів);
N та E - скінченні множини; P - скінчена
множина правил типу
![]() ,
де:
,
де:
![]() ,
,
![]() (
(![]() множина всіх слів у термінальному
алфавіті),
множина всіх слів у термінальному
алфавіті),
![]() - аксіома (виділений нетермінал).
- аксіома (виділений нетермінал).
Математичні моделі довготривалого страхування.




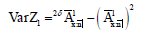



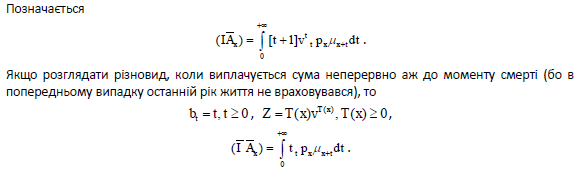
Метод функції Гріна розв’язку граничних задач.
Визначеня функції Гріна основних краєвих задач для еліптичного рівняння, представлення розв’язку.
Ф-ією
Гріна еліптичного оператора називається
узагальнена функція
![]() ,
яка задовольняє граничній задачі
,
яка задовольняє граничній задачі
 .
.
Представлення
розв‘язку, де
![]() -
номер крайової задачі.
-
номер крайової задачі.
=1
![]()
=2
![]()
=3
![]()
Визначеня функції Гріна основних краєвих задач для параболічного рівняння, представлення розв’язку.
Ф-ією
Гріна параболічного оператора називається
узагальнена функція
![]() ,
яка задовольняє граничній задачі
,
яка задовольняє граничній задачі
 .
.
Представлення розв‘язку :

![]()
Визначеня функції Гріна основних краєвих задач для гіперболічного рівняння, представлення розв’язку.
Ф-ією
Гріна гіперболічного оператора
називається узагальнена функція
![]() ,
яка задовольняє граничній задачі
,
яка задовольняє граничній задачі
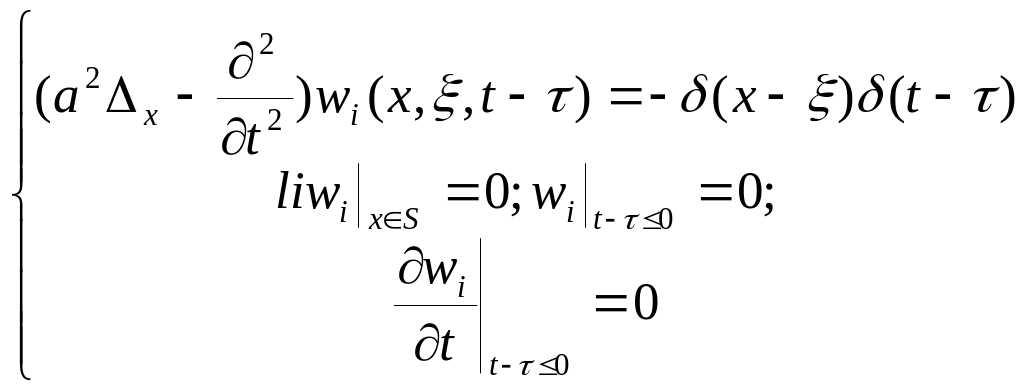 .Представлення
розв‘язку :
.Представлення
розв‘язку :

Міра Лебега та її властивості.
Система
множин
![]() називається
кільцем , якщо з
називається
кільцем , якщо з
![]() і
і
![]() ,
випливає, що
,
випливає, що
![]() та
та
![]() .
Алгеброю множин називається
кільце
.
Алгеброю множин називається
кільце
![]() ,
підмножини множини
,
підмножини множини
![]() ,
що містить
.
Кільце множин називається
,
що містить
.
Кільце множин називається
![]() -кільцем,
якщо воно разом з будь-якою послідовністю
множин
-кільцем,
якщо воно разом з будь-якою послідовністю
множин
![]() ,
,
![]() ,
…,
,
…,
![]() ,
… містить і їх об‘єднання
,
… містить і їх об‘єднання
![]() .
.
Нехай
в деякому просторі
,
задана алгебра множин
,
на
задана
функція
![]() :
:
![]() ,
,
![]() .
Функція
,
називається мірою, якщо виконуються
умови:
.
Функція
,
називається мірою, якщо виконуються
умови:
1.)
![]()
![]()
2.) Для
![]() :
:
![]() при
при
![]() і
і
![]() виконується
виконується
![]() (зліченна адитивність,
(зліченна адитивність,
![]() -
адитивність).
-
адитивність).
Властивості міри:
монотонність (якщо
 і
і
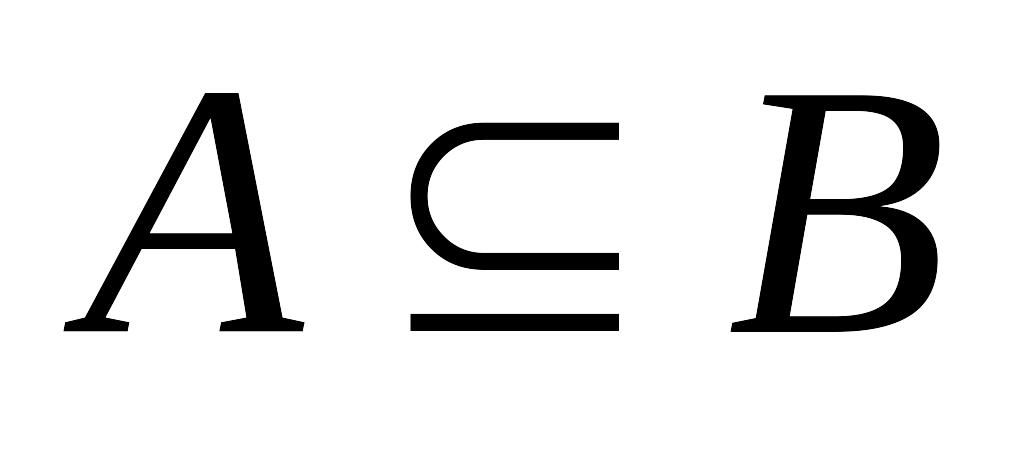
 ),
),
субтрактивність (якщо і
 ),
),
зліченна напівадитивність (Для
 і
і

 ).
).
Нехай
-
алгебра підмножин простору
,
з мірою
.
Для довільної множини
![]() існує покриття – такі
існує покриття – такі
![]() ,
що
,
що
![]() .
Функція
.
Функція
![]() :
:
![]() ;
;
![]() ,
називається зовнішньою мірою.
Властивості зовнішньої міри :
,
називається зовнішньою мірою.
Властивості зовнішньої міри :
якщо
,
то
![]() ;
невід‘ємність; монотонність; зліченна
напівадитивність.
;
невід‘ємність; монотонність; зліченна
напівадитивність.
Множина
,
називається вимірним (
-вимірним,
вимірним за Кратеодорі), якщо для
![]() виконується
виконується
![]() .
Сукупність всіх вимірних множин позначимо
через
.
Сукупність всіх вимірних множин позначимо
через
![]() ,
звуження
на
через
,
звуження
на
через
![]() .
Міра називається повною, якщо
з
.
Міра називається повною, якщо
з
![]() і
і
![]()
![]() .
.
Нехай
![]() ;
алгебра множин
;
алгебра множин
![]() -
кільцева оболонка множини всіх
напівінтервалів
-
кільцева оболонка множини всіх
напівінтервалів
![]() .
Тобто кожний елемент алгебри
,
має вигляд
.
Тобто кожний елемент алгебри
,
має вигляд
![]() .
Введемо міру
.
Введемо міру
![]() ,
як довжину складаючих
напівінтервалів
,
як довжину складаючих
напівінтервалів
![]() ,
-
зовнішня міра, побудована на мірі
.
-
вимірні множини називають вимірними
по Лебегу. Продовження міри
на
-
алгебру вимірних по Лебегу множин
називають мірою Лебега.
,
-
зовнішня міра, побудована на мірі
.
-
вимірні множини називають вимірними
по Лебегу. Продовження міри
на
-
алгебру вимірних по Лебегу множин
називають мірою Лебега.
Множина, що складається з одної точки, або скінченної множини точок вимірна, і міра її – нуль. Міра будь-якого проміжку дорівнює його довжині. Будь-яка обмежена множина вимірна по Лебегу.
Борелівською -алгеброю в довільному топологічному просторі , називається -алгебра, породжена сукупністю всіх відкритих множин з . Елементи борелівської -алгебри називаються борелівськими множинами.
