Решение задач дробно-линейного программирования симплексным методом

Задача 3.1. Найти максимальное значение функции z= на множестве решений системы ограничений

Решение. Введем обозначение:

(7)

Тогда z=

Обозначим .

Целевая функция запишется так: z=

Преобразуем систему ограничений. Умножив обе части всех ограничений на

(8)

Включим в систему ограничений (8) ограничение (7) и перейдем к переменным

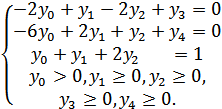(9)

Нетрудно убедиться в том, что мы получили задачу линейного программирования: найти максимальное значение z= на множестве решений системы (9).

Эту задачу линейного программирования решаем симплексным методом, обозначив и учитывая, что

Таблица 8

Базисные переменные						Свободные члены
	-2 -6 1 0	1 2 1 2	-2 1 2 -1	1 0 0 0	0 1 0 0	0 0 1 0
	0 0 1 0	3 8 1 2	2 13 2 -1	1 0 0 0	0 1 0 0	2 6 1 0
	0 0 1 0	1 0 0 0	2/3 4/3 -7/3	1/3 -8/3 -1/3 -2/3	0 1 0 0	2/3 2/3 1/3 -4/3

Имеем:

Найдем соответствующие значения

Итак, достигается при решении (2; 0; 0; 2).

Задача 3.2. Найти максимальное значение целевой функции

на множестве решений системы ограничений:

Решение. Обозначим

2

Преобразуем целевую функцию:

z = (10)

Система ограничений примет вид:

(11)

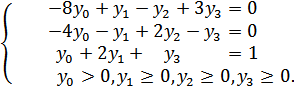
Теперь найдем наибольшее значение целевой функции (10) на множестве решений системы (11):

Таблица 9.

					Свободные члены
	-8 -4 1 0	1 2 0 1	-1 2 0 1	3 -1 1 1	0 0 1 0
	-8 -12 17 8	1 0 0 0	-1 1 2 0	3 2 -5 -2	0 0 1 0
	-20 -12 41 8	1 0 0 0	0 1 0 0	5 2 -9 -2	0 0 1 0
	0 0 1 0	1 0 0 0	0 1 0 0	25/41	20/41 12/41 1/41

при

Заметим, что если бы в оптимальном плане был бы равен 0, то 2 при оптимальном базисном решении стремилось бы к бесконечности. Отсюда следует неограниченность множества решений системы ограничений. В этом случае глобальный максимум z (конечный или бесконечный) достигается в бесконечно удаленных точках.