2. Примеры решение задач линейного программирования в пакете Lingo
Пакет LINGO решает задачи линейного, нелинейного и целочисленного программирования. LINGO предоставляет большую гибкость в записи модели.
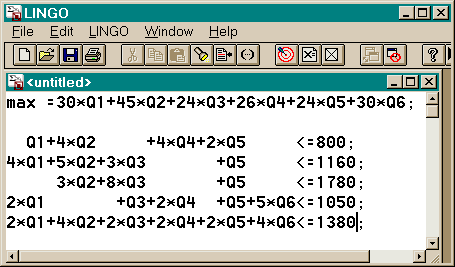
2.1. Изготовление продукции из нескольких компонент
Задача. Изготовитель производит 6 продуктов из 6 материалов. На каждый продукт требуется различная комбинация исходных материалов в определенной пропорции.
Известна прибыль, получаемая от продажи единицы каждого из продуктов.
Задано наличие (на складе) каждого из исходных материалов, которое не может быть превышено при изготовлении исходной продукции.
В таблице приведены числовые данные задачи:
Таблица 11
Продукты |
1 |
2 |
3 |
4 |
5 |
6 |
Запасы |
|
м а т е р и а л ы |
сталь |
1 |
4 |
- |
4 |
2 |
- |
800 |
дерево |
4 |
5 |
3 |
- |
1 |
- |
1160 |
|
пластмасса |
- |
3 |
8 |
- |
1 |
- |
1760 |
|
резина |
2 |
- |
1 |
2 |
1 |
5 |
1050 |
|
стекло |
2 |
4 |
2 |
2 |
2 |
4 |
1360 |
|
краска |
1 |
4 |
1 |
4 |
3 |
4 |
1240 |
|
Прибыль на единицу продукции |
30 |
45 |
24 |
26 |
24 |
30 |
|
|
Необходимо максимизировать прибыль, которая может быть получена от продажи указанных продуктов, не превышая имеющихся запасов исходных материалов.
Решение.
Математическая формулировка задачи.
Если обозначить через Q1, Q2, …,Q6 соответственно количество продукции 1-го, 2-го и т.д. типов, то целевая функция, подлежащая оптимизации запишется как
Ограничения определяются тем, что имеющиеся запасы исходных материалов не могут быть превышены. Известно, сколько расходуется каждого материала (например, стали) на каждый вид продукции, то общий расход стали будет равен Q1+4Q2+4Q4+2Q2. Следовательно, ограничение по стали будет иметь вид:
Аналогично для остальных материалов ограничения запишутся в виде:
Для решения задачи на экране LINGO наберите следующий текст (фактически повторяющий вышеприведенную формальную постановку задачи):
И
нажмите кнопку
Можно также воспользоваться командой
меню: LINGO/Solve.
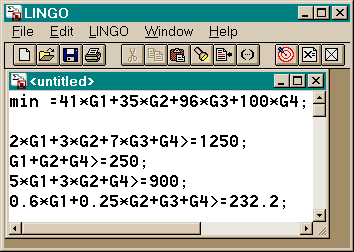
2.2. Изготовление смеси
Рацион для животных фермы составляется как смесь нескольких питательных кормов G1,G2,G3,G4.
Каждый из этих кормов включает в себя необходимые для роста и здоровья животных вещества A,B,C,D. Состав каждого корма (сколько в нем находится веществ A,B,C,D) задан в таблице. Известна цена единицы каждого из кормов. Каждое из веществ должно присутствовать в рационе не менее некоторого количества, необходимого для нормального развития животных (Этот необходимый минимум приведен также в таблице). Необходимо минимизировать цену кормовой смеси.
Таблица 12.
|
Корм1 |
Корм1 |
Корм3 |
Корм4 |
Минимум в-ва |
Вещество A |
2 |
3 |
7 |
1 |
1250 |
Вещество B |
1 |
1 |
0 |
1 |
2500 |
Вещество C |
5 |
3 |
0 |
1 |
900 |
Вещество D |
0,6 |
0,25 |
1 |
1 |
232,5 |
Цена/единицу корма |
41 |
35 |
96 |
100 |
|
Решение.
Таблица 13
Математическая постановка задачи |
Запись задачи в LINGO |
Целевая функция:
Ограничения:
|
|
