6. Метод случайных испытаний

Пусть каким- либо способом выбрано n случайных чисел. Принимаем эти числа за значения переменных х₁, х₂, х₃, …,х_n, проверяем допустимость такого решения и вычисляем для него значение целевой функции. Такой процесс повторяем многократно, фиксируя точку в этом случае, если целевая функция в ней достигает лучшего по сравнению с предыдущим значения(в смысле приближения к оптимуму).

Общее число случайных проб зависит от числа переменных, требуемой точности искомых величин и заданной вероятности получения оптимального решения. Все это определяется заранее. Поиск прекращается, когда число точек достигнет расчетного. Точку с наибольшим ( наименьшим) значением целевой функции считаем оптимальной.

Метод случайных испытаний может быть реализован только на ЭВМ, причем интересно отметить, что случайные величины числа ЭВМ вырабатывает сама.

3. Решение задач оптимизации с помощью пакетов прикладных программ

1. Пример решения транспортной задачи в среде ms Excel

Задача. Пусть производство продукции осуществляется на 4-х предприятиях А₁, А₂, А₃, А₄ а затем развозится в 5 пунктов потребления этой продукции B₁, B₂, B₃, B₄, B₅. На предприятиях A_i (i = 1, 2, 3, 4) продукция находится соответственно в количествах a_i (условных единиц). В пункты B_j (j = 1, 2, 3, 4,5) требуется доставить b_j единиц продукции. Стоимость перевозки единицы груза (с учетом расстояний) из A_i в B_j определена матрицей .

Предприятия могут выпускать в день 235, 175, 185 и 175 единиц продукции. Пункты потребления готовы принимать ежедневно 125, 160, 60, 250 и 175 единиц продукции. Стоимость перевозки единицы продукции (в у. е.) с предприятий в пункты потребления приведена в таблице.

Таблица 10

Предприятия	Потребители					Объемы производства
	B1	B2	B3	B4	B5
A1	3,2	3	2,35	4	3,65	235
A2	3	2,85	2,5	3,9	3,55	175
A3	3,75	2,5	2,4	3,5	3,4	185
A4	4	2	2,1	4,1	3,4	175
Потреб-ности	125	160	60	250	175

Требуется минимизировать суммарные транспортные расходы по перевозке продукции.

Решение.

Необходимо выполнить следующее:

1. Установить, является ли модель транспортной задачи, заданная таблицей, сбалансированной.

2. Разработать математическую модель задачи.

3. Найти минимальную стоимость перевозок, используя надстройку «Поиск решения» в среде MS Excel.

Решение.

1. Выполним проверку сбалансированности математической модели задачи. Модель является сбалансированной, так как суммарный объем производимой продукции в день равен суммарному объему потребности в ней:

235+175+185+175=125+160+60+250+175

(При решении этой задачи не учитываются издержки, связанные со складированием и недопоставкой продукции).

2. Приступим к построению математической модели поставленной задачи. Неизвестными будем считать объемы перевозок.

Пусть х_ij – объем перевозок с i-го пункта поставки в j-й пункт потребления. Суммарные транспортные расходы – это функция , где с_ij – стоимость перевозки единицы продукции с i-го предприятия в j-й пункт потребления .

Неизвестные в этой задаче должны удовлетворять следующим ограничениям:

• Объемы перевозок не могут быть отрицательными, т. е. ;

• Поскольку модель сбалансирована, то вся продукция должна быть вывезена с предприятий, а потребности всех пунктов потребления должны быть полностью удовлетворены, т. е. 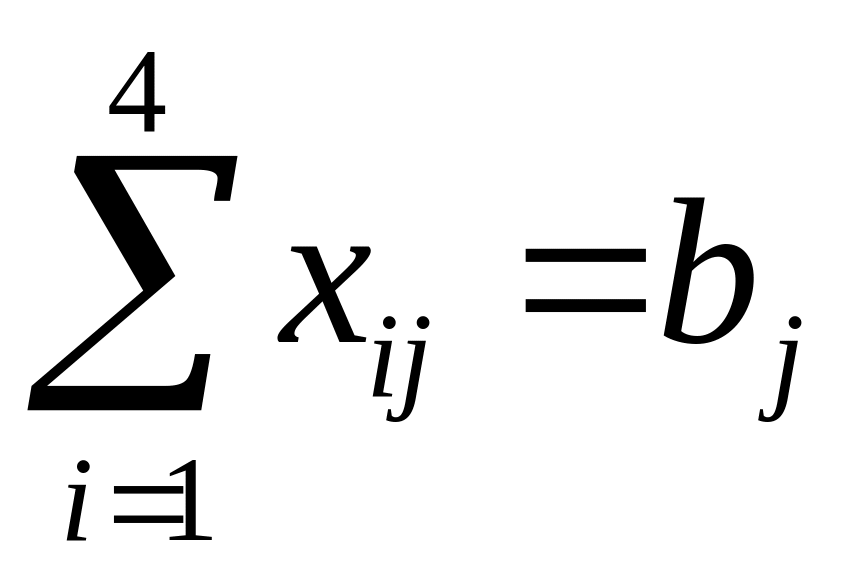и .

Итак, имеем следующую задачу ЛП:

найти минимум функции:

при ограничениях:

,

3. Приступаем к решению задачи на компьютере.

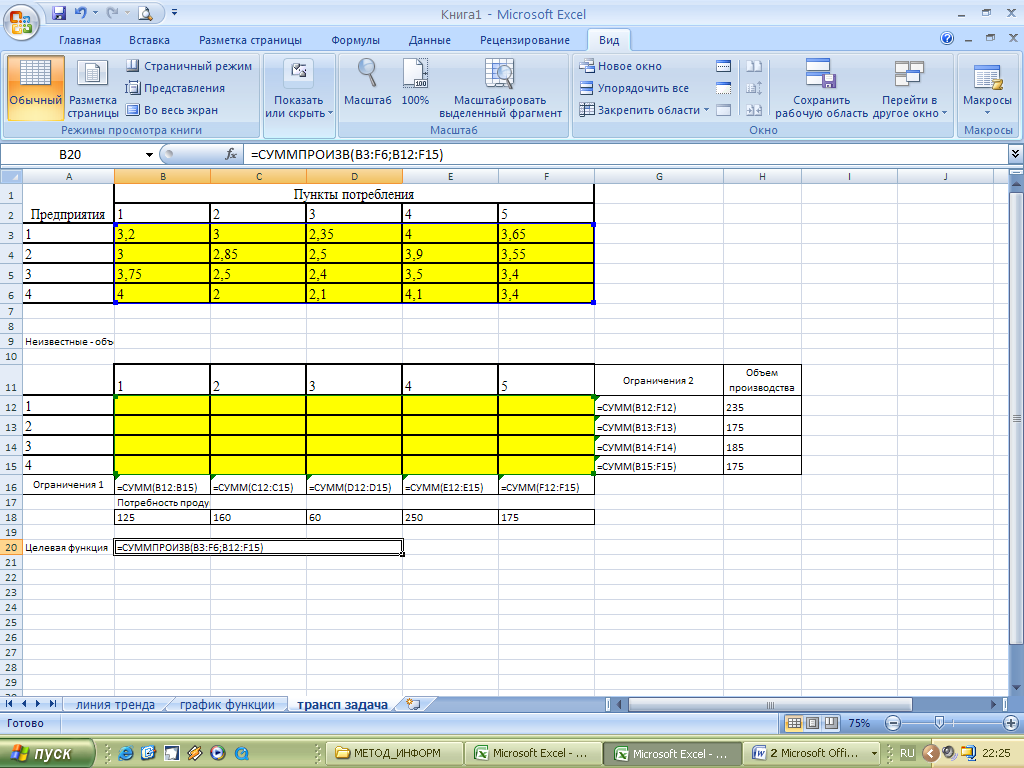
3.1. Откроем новый рабочий лист Excel.

3.2. В ячейки B3:F6 стоимость перевозок единицы груза.

3.3. В ячейках B16:F16 укажем формулы для расчета суммарной потребности продукции для j-го пункта, в ячейках G12:G15 – формулы суммарного объема производства i-го предприятия.

3.4. В ячейки B18:F18 заносим значения потребности продукции соответствующего пункта потребления, в ячейки H12:H15 заносим значения объема производства соответствующего предприятия.

3.5. В ячейку B20 занесем формулу целевой функции.

3.6. Выполним команду Сервис → Поиск решения. Откроется диалоговое окно Поиск решения.

3.7. В поле Установить целевую ячейку указываем ячейку, содержащую оптимизируемое значение. Установим переключатель Равный в положение минимальному значению.

3.8. В поле Изменяя ячейки мышью зададим диапазон подбираемых параметров $B$12:$F$15.

3.9. В поле Ограничения введем необходимые ограничения и нажмем на кнопку Добавить, затем Выполнить.

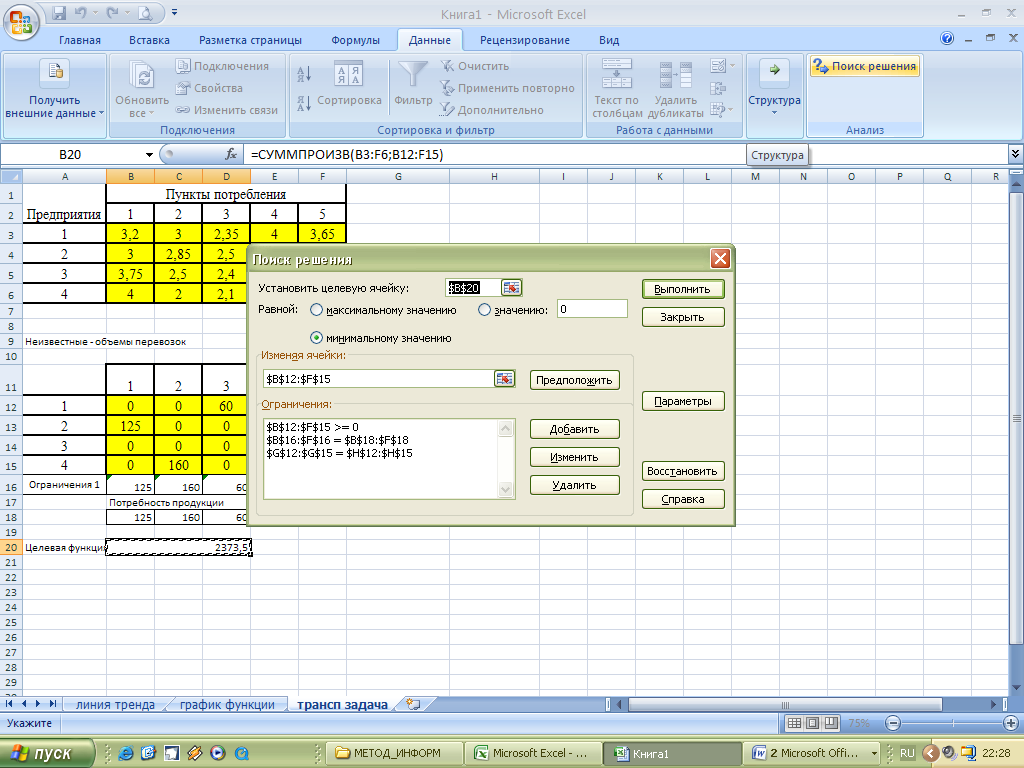
В результате получится оптимальный набор переменных при данных ограничениях:

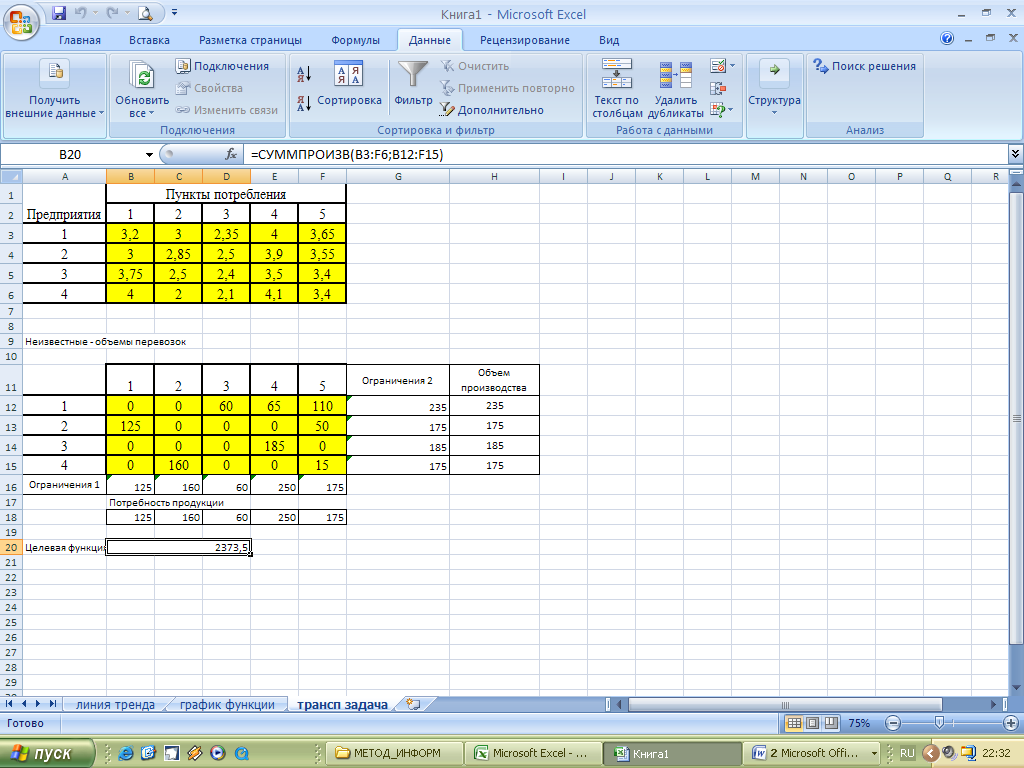
Оптимальность решения можно проверить, экспериментируя со значениями ячеек $B$12:$F$15.