6. Теорема Дебре о функции полезности. Свойства функции полезности: возрастание по каждому аргументу и закон Госсена (на примере логарифма Бернулли).

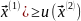Теорема Дебре: если отношение предпочтения потребителя (rwp) транзитивно, непрерывно и удовлетворяет аксиоме ненасыщаемости, то существует непрерывная на пространстве благ С скалярная функция( обозначим ее U), которая возрастает по каждому аргументу, такая что, rwp ( =A то u( . Если наборы благ безразличны, то неравенство превращается в равенство.

Свойства функции полезности:

1)Непрерывность

2)Дифференцируемость

3)Убывание предельной полезности

4)Возрастает по каждому аргументу

5)Выпукла вверх

Конкретно рассмотрим свойство 4. Возрастание потребления одного при неизменном потреблении другого продукта ведет к росту потребительской оценки (возрастанию функции полезности).

.

Первые частные производные называются предельными полезностями продуктов.

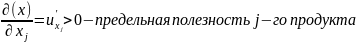
Теперь обратимся к свойству 3. Предельная полезность каждого продукта уменьшается, если объем его потребления продолжает расти при неизменном потреблении остальных. Это свойство называется законом убывания предельной полезности (закон Госсена). Это следует из аксиомы выпуклости.

Можно сказать, что функция полезности строго вогнута, то есть полезность любого товар уменьшается по мере его потребления.

Рассмотреть на логарифме Бернулли.

u=a₁*ln(x₁-c₁)+…+a_n*ln(x_n-c_n)

x_i>c_i ,c_i≥0, a_i≥0

7. Теорема Дебре о функции полезности. Свойства функции полезности: выпуклость вверх (на примере неоклассической функции полезности).

Теорема Дебре: если отношение предпочтения потребителя (rwp) транзитивно, непрерывно и удовлетворяет аксиоме ненасыщаемости, то существует непрерывная на пространстве благ С скалярная функция( обозначим ее U), которая возрастает по каждому аргументу, такая что, rwp ( =A то u( . Если наборы благ безразличны, то неравенство превращается в равенство.

Функция полезности является дважды дифференцируемой и имеет непрерывные частные производные. Ее матрица Гессе, состоящая из вторых производных, отрицательно определена. Это означает, что функция полезности строго вогнута.

8. Теорема Дебре о функции полезности. Свойства функции полезности: кривые безразличия и предельные нормы замещения благ (на примере неоклассической функции полезности).

Теорема Дебре: если отношение предпочтения потребителя (rwp) транзитивно, непрерывно и удовлетворяет аксиоме ненасыщаемости, то существует непрерывная на пространстве благ С скалярная функция( обозначим ее U), которая возрастает по каждому аргументу, такая что, rwp ( =A то u( . Если наборы благ безразличны, то неравенство превращается в равенство.

Х₂

Л иния, соединяющая потребительские наборы ( ), имеющие один и тот же уровень удовлетворения потребностей потребителя, называется линией безразличия. Это есть линии уровня функции полезности.

Множество линий безразличия называется карта линий безразличия. Каждая кривая представляет собой наборы потребительских товаров и услуг, которые человек оценивает одинаково.

Свойства функции полезности означают, что линия безразличия убывает и строго выпукла к началу координат.

Х₁

Лемма: кривые безразличия не могут пересекаться.

Количество денежных средств, которыми располагает потребитель, ограничено, поэтому он должен искать компромисс, когда делает выбор между товарами, и кривые безразличия могут помочь. Перемещаясь вдоль кривой безразличия сверху вниз, видно, что потребитель котов отказаться от определенного количества единиц потребляемого товара в пользу товара . Чтобы количественно определить, каким объемом того или иного товара потребитель готов пожертвовать ради увеличения потребления другого товара, используется предельная норма замещения.

– норма замещения первого продукта вторым на потребительском наборе ( )

– предельная норма замещения первого продукта вторым.