21

ВВЕДЕНИЕ

Пространственной фототриангуляцией называют метод камерального сгущения съемочного обоснования путем построения и уравнивания фотограмметрической сети. Координаты точек, получаемые в результате уравнивания сети, используются для составления топографических карт, планов, фотопланов и иных документов. Основной целью пространственной триангуляции является максимальное сокращение объема полевых геодезических работ.

Аналитическая фототриангуляция основана на использовании строгих математических зависимостей между координатами точек аэроснимка и местности. Ее построению предшествует измерение координат и параллаксов точек снимков на высокоточных стереокомпараторах, а использование ЭВМ для их обработки открывает возможности как учета всех искажений точек, выражающихся математическими зависимостями, так и применения строгих методов уравнивания результатов измерений методов наименьших квадратов.

Необходимость сгущения планового обоснования в пределах коротких маршрутов может возникнуть также при создании фотопланов с использованием плановой привязки прежних лет, при обновлении или корректуре старых фотопланов и в других случаях.

Работы такого рода не являются массовыми и в настоящее время их выполняют, главным образом, методом графической фототриангуляции, точность которой невелика.

В результате выполнения расчетно-графической работы студентом будут закреплены навыки использования ЭВМ для обработки результатов измерений, получены геодезические координаты главной и четырех трансформационных точек на каждый аэроснимок маршрута.

1. Вычисление центральных углов, образованных направлениями на связующие, трансформационные и геодезические точки

Вычисление центральных углов, образованных направлениями на связующие, трансформационные и геодезические точки осуществляется по формуле

cos θ = 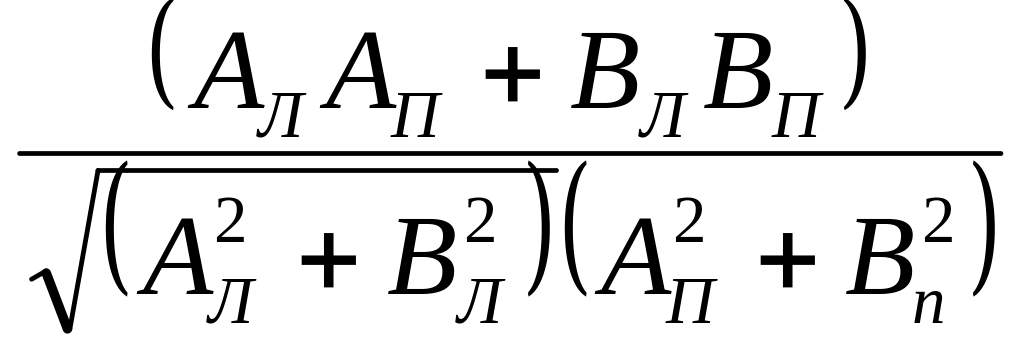(1)

где А_л,п=У_л,п-У_в;

В_л,п=-(Х_л,п - Х_в);

Х_л,п; У_л,п – отсчеты по шкалам стереокомпаратора на точки, определяющие левое и правое направления угла;

Хв, Ув- отсчеты на вершину угла.

Расчеты по приведенной формуле выполняют с помощью программы Simplex (рисунок 1).

Исходные данные для расчетов выполняются сначала для контрольного примера. Порядок ввода данных и их значения для контрольного примера приведены в таблице 1.

Таблица 1 – Порядок ввода исходных данных для контрольного примера

Вводимая величина	Значение
ХВ	84,39
YВ	-3,14
рВ	82,092
qВ	-4,485
ХЛ	2,09
YЛ	-2,85
pЛ	78,140
qЛ	-5,827
ХП	42,94
YП	37,54
pП	79,730
qП	-4,760

При вводе исходных данных необходимо ввести число ограничений – 12, переменных – 12. (Для контрольного примера число ограничений – 12, переменных – 1.)

Рисунок 1 – Пример ввода исходных данных контрольного примера

После ввода данных необходимо сохранить их и получить решение (рисунок 2).

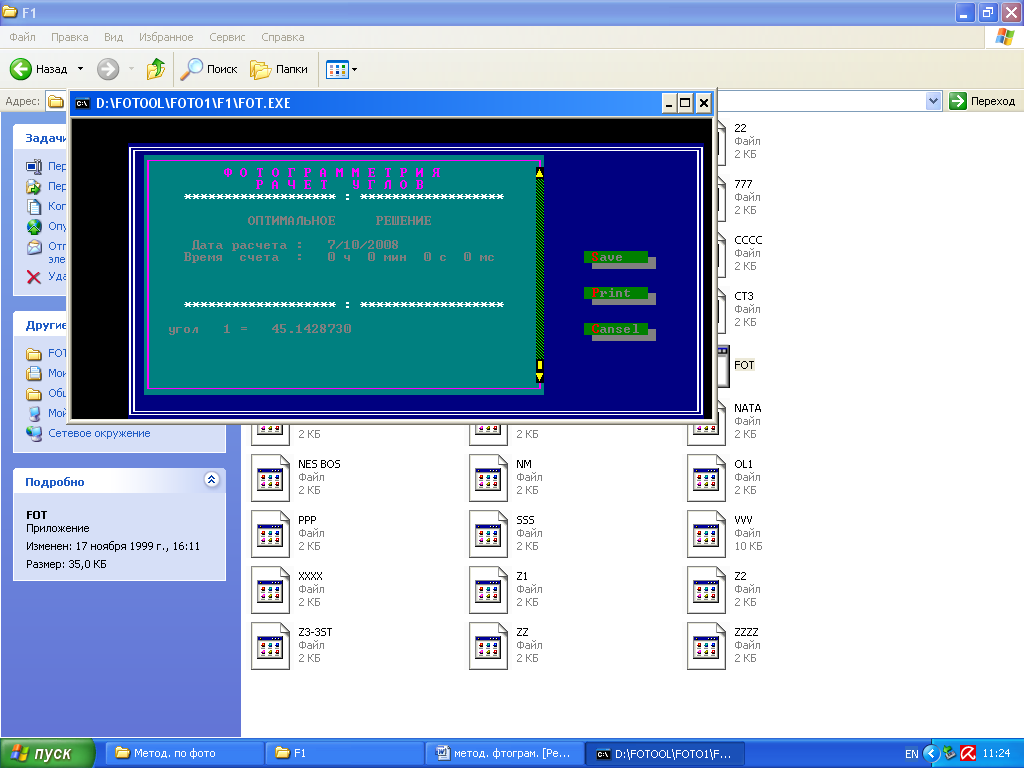
Рисунок 2 – Результат решения контрольного примера

Результаты вычисления выписывают в журнал-схему (рисунок 3), которую составляют для каждой стереопары.

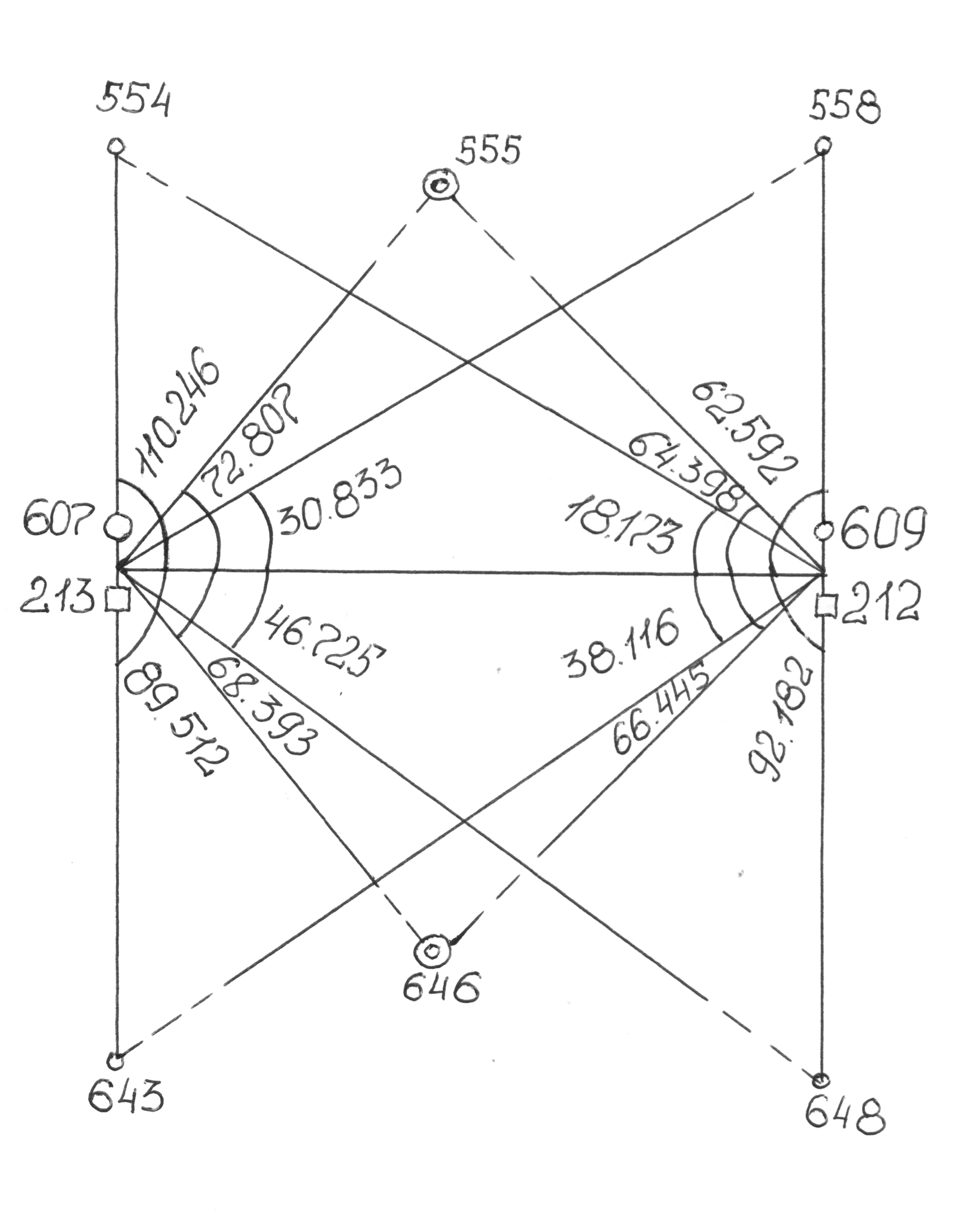
Рисунок 3 – Журнал-схема определения центральных углов на стереопаре 213-212

2. Уравнивание углов в ромбических сетях

Каждый ромб представляет собой центральную систему (рисунок 4), в которой возникает четыре условия фигур, условие горизонта и полюсное условие. Уравнивание за условия фигур не выполняют, так как углы γ=180-(α+β). Условное уравнение горизонта состоит в том, что сумма углов βi должна быть равной 360°. В противном случае β1+β2+β3+β4-360 =Wr. Поправка в каждый угол V_βi=- .Чтобы не нарушалось условие фигур, в углы α₁ и γ₂ вводят поправки

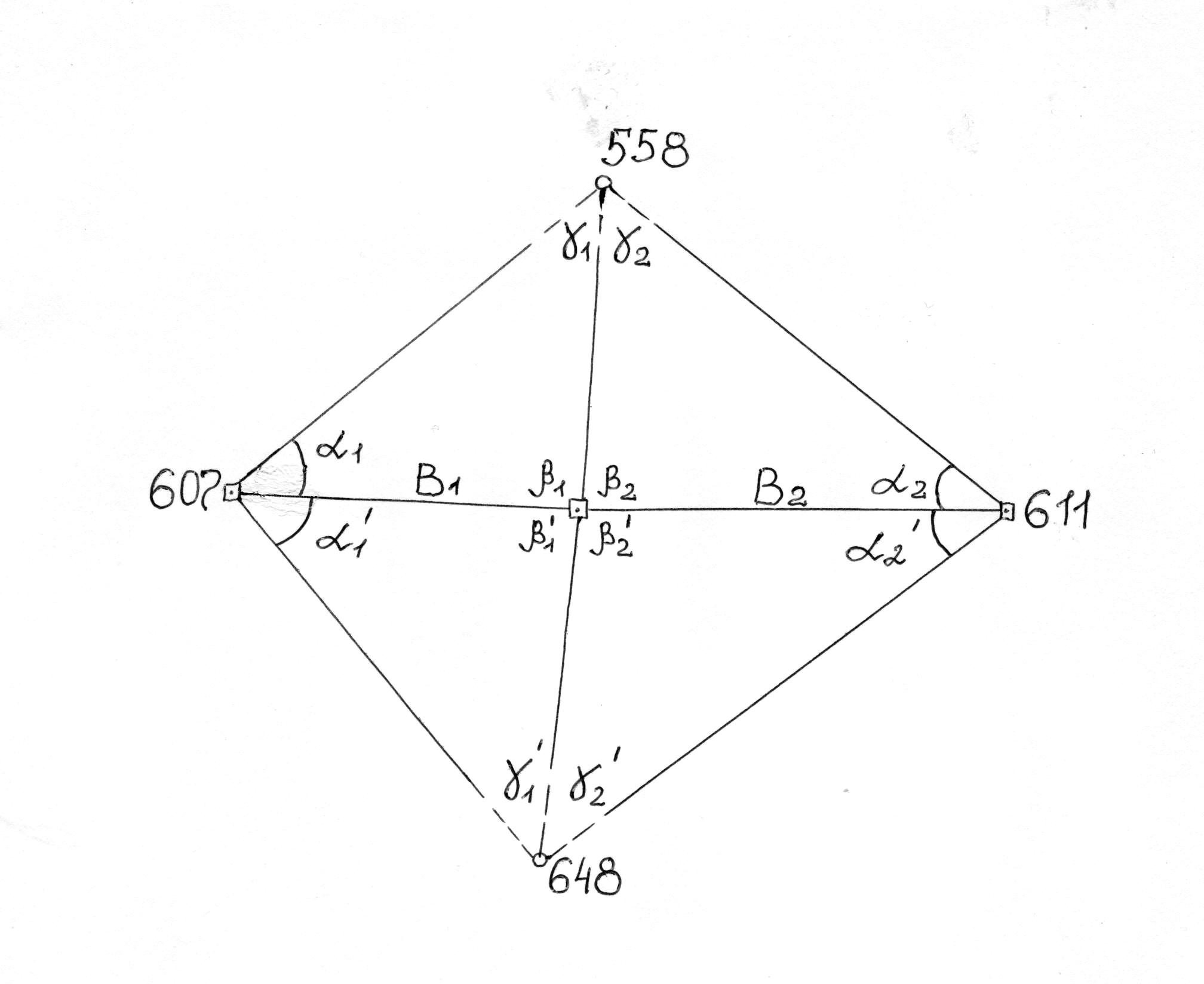
Рисунок 4 – Составление условных уравнений в ромбической сети

Полюсное условное уравнение для ромбической сети в линейном виде выглядит:

δ_α1V_α1-δ_γ1V_γ1+δ_γ2V_γ2-δ_α2V_α2+δ_α2V_α2-δ_γ2V_γ2+δ_γ1V_γ1-δ_α1V_α1+W_п=0,

где , W_п= (

Для съемочной сети поправки в углы α_i и γ_i равными, получим . Значения поправок, свободных членов и их допустимых значений вычисляют с помощью программы Simplex (рисунок 1).

Исходные данные для расчетов выполняются сначала для контрольного примера. Порядок ввода данных и их значения для контрольного примера приведены в таблице 2.

Таблица 2 – Порядок ввода исходных данных для контрольного примера

Вводимая величина	Значение
α1	63,435
γ2	53,130
α2/	30,965
γ1/	36,870
γ1	45,00
α2	50,906
γ2/	45,00
α1/	34,695

При вводе исходных данных необходимо ввести число ограничений – 8, переменных – 5. (Для контрольного примера число ограничений – 8, переменных – 1.)

После ввода данных необходимо сохранить их и получить решение (рисунок 2).

Решение: W_П⁰ = 8,0787×10^-4, V⁰ =9,4966×10^-5, W_Пдоп = 9^'5410371.

Уравнивание углов в каждом ромбическом звене выполняют на отдельной схеме (рисунок 5).

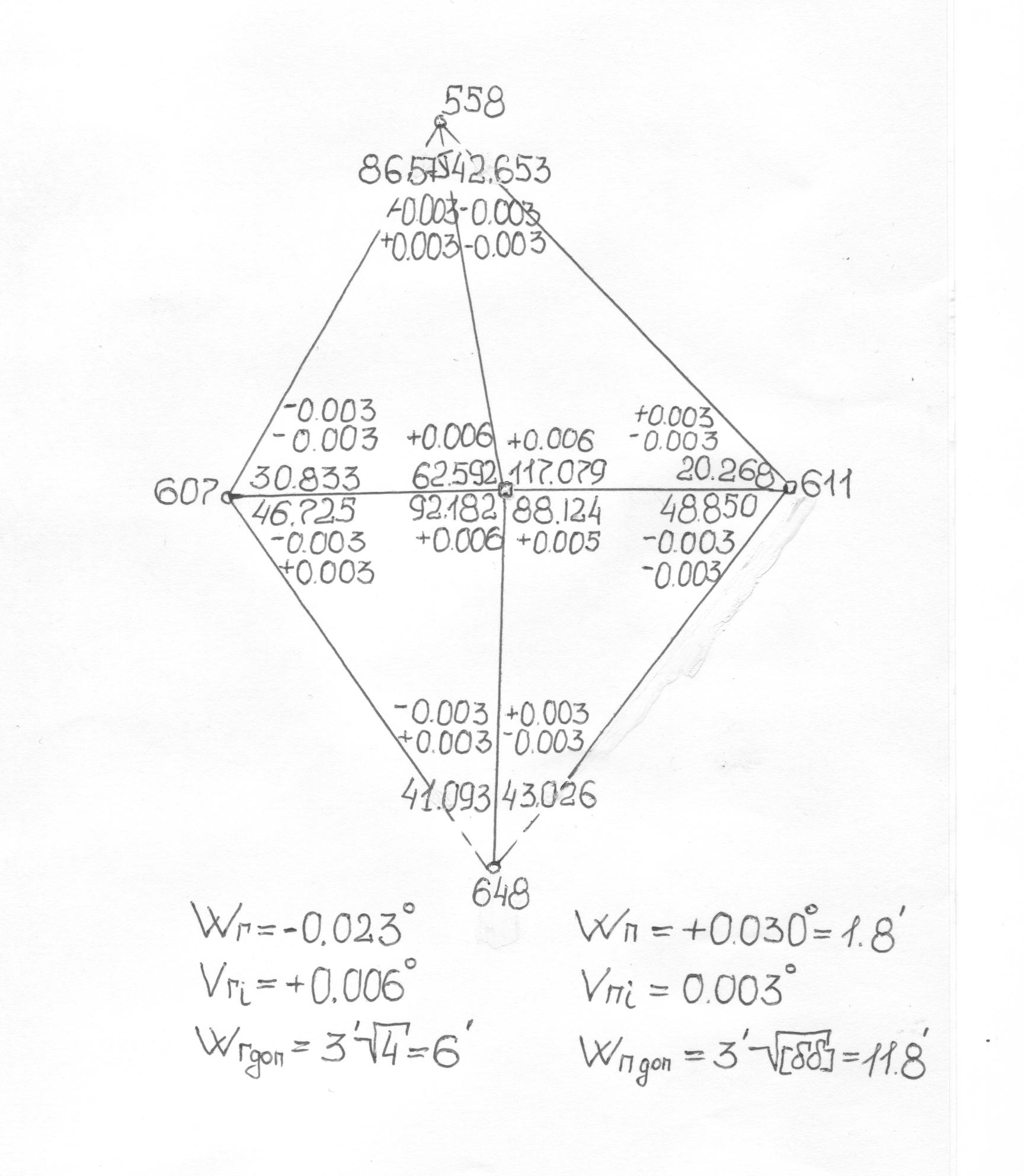
W_Г=-0,023⁰, V_Гi=+0,006⁰, W_Гдоп=3' =6'

W_П=+0,030⁰=1,8', V_Пi=+0,003⁰, W_Пдоп=3' =11,8'

Рисунок 5 – Уравнивание углов в ромбической сети