4. Особые виды кинематических структур

В коробке передач общее число ступеней

z = p₁ p₂ ... p_r-1 p_r,

где р₁...р_r - числа передач, составляющих отдельные группы, которые связывают соседние валы. Если р_r - последняя переборная группа в кинематическом порядке, а х_r - ее характеристика, то, по общему правилу, величина х_r равна произведению числа передач по всех кинематически предшествующих группах:

x_r = p₁ p₂ ... p_r-1 = z : p_r

Наиболее целесообразно принимать р_r = 2; тогда х_r = z/2. Подставив эти значения в формулу (4), получим:

R_r = ^(pr-1)xr = ^z/2

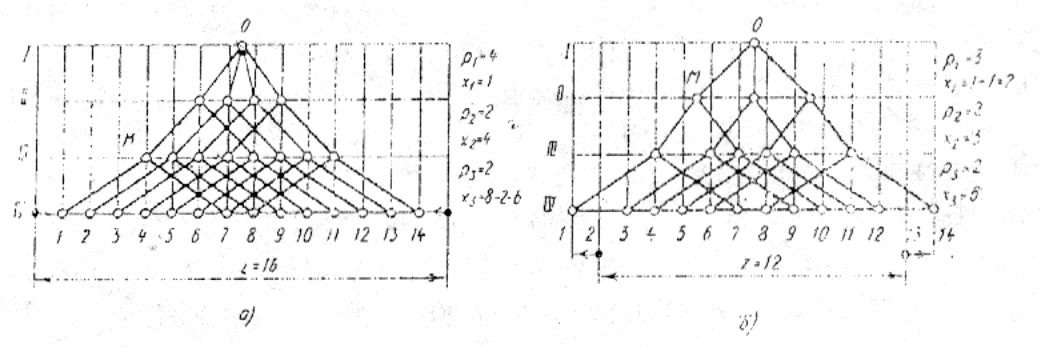
Рис 4.1. Сетка для структуры с совпадением скоростей (а) и для структуры с “выпадением” скоростей (б)

Исходя из известного ограничения R_p < 8, должно быть

^z/2 < 8; ^z < 64; ^z/ < 64/; ^z-1 < 64/. (4.2)

Последнее неравенство является условием, которое показывает, можно ли обеспечить данный диапазон регулирования при обычной множительной структуре. Например, при  = 1,25 должно быть R_n < 50. Если условие не соблюдается, использует особые виды структур, позволяющие реализовать большие значения R_n. В частности, в токарных станках требуется R_n = 100, а иногда и более. Особыми являются структуры с совпадением или "выпадением" (пропуском) скоростей и сложенные структуры.

Рассмотрим пример, когда R_n = 120 и  = 1,4. По этим данным получается z = 14, содержащее обычно неудобный множитель 7. Структура с совпадением скоростей обеспечивает заданный диапазон и вычисленное z. Предварительно примем формулу структуры z = 16 = 4₁ · 2₁ · 2₃. Но построим сетку для z = 14. Сжатие 16 ступеней в пределы 14 интервалов шкалы приводит к совпадению (повторению) скоростей на двух ступенях (рис. 4.1, а) Построение ведут, как обычно, от точки 0. По достижении точки М определяют, насколько должна быть уменьшена характеристика последней переборной группы.

Тот же большой диапазон R_n можно обеспечить, уменьшив число ступеней до z = 12 = 3₁ · 2₂ · 2₃, но заготовив сетку с 14 интервалами шкалы. Растягивание 12 ступеней на 14 интервалов приводит к "выпадению" двух скоростей (рис. 4.1, б) Построение ведут сначала от точки 1, проводя крайние левые лучи, как для графика частот вращения, но учитывая симметрию и руководствуясь значениями р и х . Дойдя до точки М, определяют, насколько должна быть увеличена характеристика основной группы, чтобы попасть в точку 0. Затем достраивают сетку в обычном порядке. Структуру с "выпадением" скоростей называют также структурой с ломаным (неравномерным) рядом. Большая, средняя, часть ряда, которая используется наиболее часто, построена со знаменателем . По концам ряда знаменатель больше (на рис. 4.1, б - ² так как 2lg=lg²)

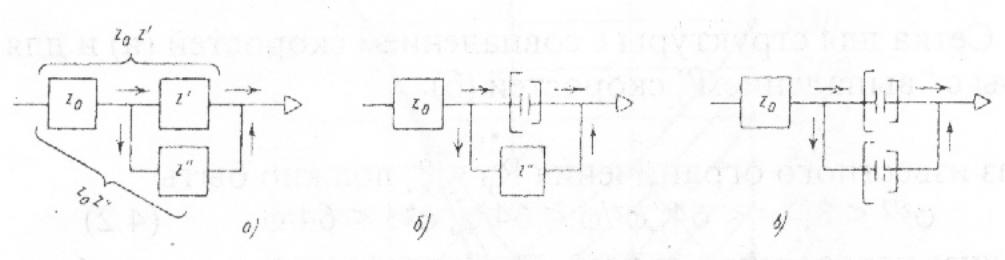
Рис. 4.2. Варианты структурных схем сложенной структуры.

4.1. Сложенные структуры. Обозначим через z₀ число ступеней скорости, создаваемых рядом последовательно соединенных групп передач (рис. 4.2, а), через z' и z" - числа ступеней, которые обеспечиваются другими частями структуры. Каждая из этих частей также представляет собой одну или несколько групп передач, соединенных последовательно.

Рассмотрим совместно части z₀ и z' , соединенные между собой также последовательно. Вместе они составляют множительную структуру, не отличающуюся принципиально от структуры каждой части в отдельности, и обеспечивают z₀ z' ступеней скорости (при этом часть структуры с z" не используется, выключена). При включении z" (часть структуры с z' должна быть выключена) таким же образом может быть получено z₀ z'' ступеней скорости. Структура, состоящая из последовательно и параллельно соединенных групп передач, называется сложенной (рис. 4.2). Общее число скоростей при такой структуре z = z₀ z' + z_{0 z}'' = z₀ (z' + z'').

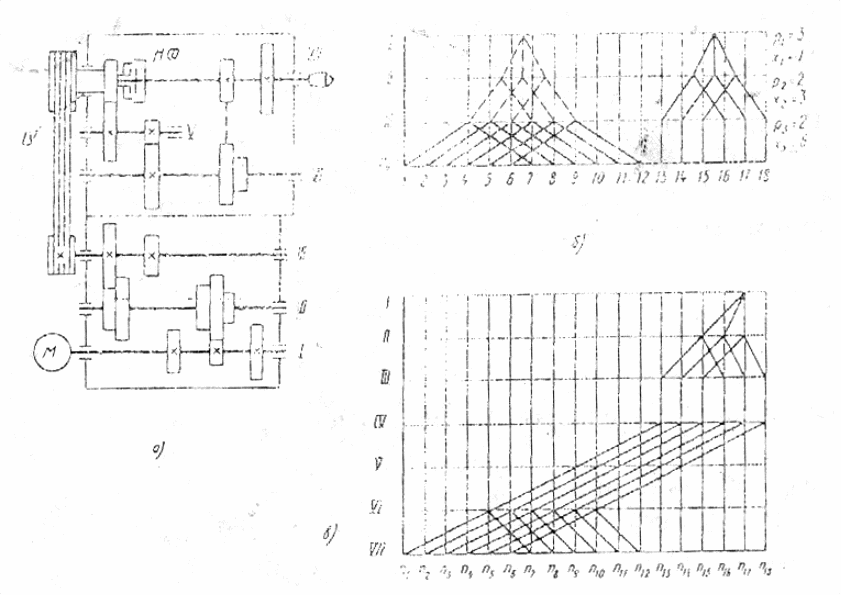
Рис. 4.3. Коробка скоростей со сложенной структурой :

а - кинематическая схема; б - структурная схема; в - график частот вращения.

В частном случае (рис. 4.2,б) может быть z' = 1; тогда z = z₀ (1 + z"). При z' = z" = 1 (рис. 4.2, в) сложенная структура оказывается структурой с одинарным перебором, которая обеспечивает z₀ (1 + 1) =2z₀ скоростей .

Как и все особые виды структур, сложенные структуры позволяют охватить большие диапазоны регулирования скоростей и получить число ступеней, кратное не только двум и трем, на и пяти или семи (z' +z"). Кроме того, важнейшее достоинство сложенной структуры состоит в том, что исключаются из работы при высоких скоростях передачи одной из ·параллельных ветвей. Это снижает потери на трение, увеличивает точность обработки, позволяет изменять тип шпиндельной передачи (ременная передача при высоких частотах вращения и зубчатая передача при низких частотах - рис. 4.3, а).

На рис. 4.3,а представлена сложенная структура, отвечающая формуле z = 18 = 3₁ - 2₂ (1 + 2₃). На выходе коробки скоростей (вал III) получают шесть ступеней. Нижние 2/3 диапазона регулирования частоты вращения шпинделя обеспечиваются через двойной перебор при выключенной муфте МФ. Верхняя треть частот вращения шпинделя VII получается от шкива на валу IV напрямую через муфту МФ (блок колес на валу VI должен быть выключена.

Структурную сетку и график частот вращения строят по обычным правилам (рис. 4.3 , б, в). В сетке общую часть структуры z₀ = 3₁ - 2₂ показывают дважды или второе изображение подразумевают (на рис. 4.3,б показано пунктиром). Характеристику x₃ группы передач перебора получают, рассматривая эту группу как продолжение множительной структуры общей части z₀.