Содержание

1. Введение............................................................................................3

2. Постановка задачи…………………………………………...…….5

3. Прямой алгоритм……………………………………………….....13

4. Список литературы………………………………………………..17

5. Приложение №1. Структурное проектирование…………...…...17

6. Приложение №2. Текст программы…………...…………………17

7. Приложение №3……...……………………………………………17

1. Введение

Благодаря своему широкому применению, теория о нахождении кратчайших путей в последнее время интенсивно развивается. Нахождение кратчайшего пути жизненно необходимо и используется практически везде, так же в построении дорог.

 Для решения задач такого типа - используются методы динамического программирования, теории графов, о которых пойдет речь в данной работе.

Очень много задач решаются методами теории графов. Приведем несколько примеров.

1. Пусть мы имеем карту дорог, в которой для каждого города указано расстояние до всех соседних с ним. Здесь два города называются соседними, если существует дорога, соединяющая непосредственно эти два города.

2. Аналогично, можно рассмотреть улицы и перекрестки внутри одного города. Заметим, что могут быть улицы с односторонним движением.

3. Сеть компьютеров, соединенных проводными линиями связи.

4. Устройство, состоящее из микросхем, соединенных друг с другом наборами проводников.

5. Генеалогические деревья, указывающие родственные отношения между людьми, и т.д.

Теория графов - это область дискретной матема­тики, особенностью которой является геометрический подход к изучению объектов. Основной объект теории графов-граф и его обобщения.

Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

В курсовой работе будет рассматриваться задача о проведении дорог. Нам нужно сделать, что бы дороги, которые мы хотим проложить через города или улицы, по километражу были максимально короткими. В результате будет потрачено меньше времени и средств на строительство дорог.

Это го результата можно добиться при помощи разных алгоритмов и методов, например:

1. Алгоритм Дейкстры;

2. Алгоритм Флойда-Уоршелла;

3. Алгоритм Форда-Беллмана;

4. Расстановка меток;

5. Коммуникационная сеть минимальной длины (дерево кратчайших расстояний), и т.д.

В данной работе мы будем рассматривать последний метод, т.е. коммуникационная сеть минимальной длины (дерево кратчайших расстояний).

Коммуникационная сеть минимальной длины (или дерево кратчайших расстояний) – это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети, то есть возможность попасть из любого узла в любой другой узел. Целью работы является изучение метода решения поставленной задачи и написание программы, которая реализует данный метод и позволяет находить кратчайший путь между городами или улицами .

2. Постановка задачи

Рассмотрим задачу о проведении дорог, как задачу на графах.

Теория графов — раздел дискретной математики, изучающий свойства графов.

Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие или вновь проектируемые дома, сооружения, перекрёстки, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут. 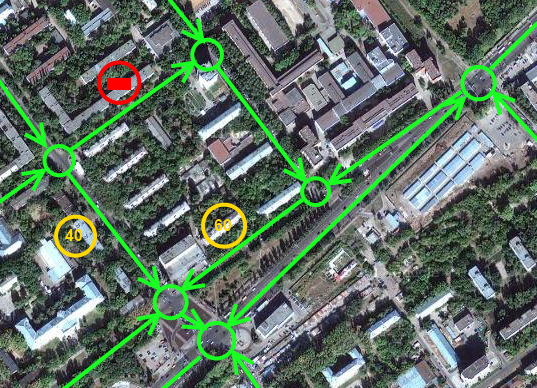Рис.1 Представление участка в виде графа.

Граф — базовое понятие. Оно включает множество вершин и множество рёбер, являющееся подмножеством декартова квадрата множества вершин (то есть каждое ребро соединяет ровно две вершины).

Граф является ориентированным, если для каждого ребра задано направление, в котором возможно движение по этому ребру. Если движение возможно в обоих направлениях, то граф называется неориентированным.

Рис. 2

Граф называется взвешенным, если каждому ребру поставлено в соответствие некоторое число (вес).

Граф называется связным, если из любой его вершины существует путь (не обязательно состоящий из одного ребра) в любую другую.

На рисунке 2 изображен неориентированный, несвязный, невзвешенный граф.

Часть графа, которая является связной, называется компонентой связности. В графе, изображенном на рисунке две компоненты связности.

Степенью вершины (в неориентированном графе) называется количество выходящих из нее ребер.

Рис 3

Петлей называется ребро, соединяющее вершину с самой собой, показано на рисунке 3.

Простым путем в графе называется путь, в котором ни одно ребро не встречается дважды.

Циклом называется путь, не проходящий дважды через одну и ту же вершину.

Пустым называется граф без рёбер.

Полным называется граф, в котором каждые две вершины смежные. Конечная последовательность необязательно различных рёбер E₁,E₂,...E_n называется маршрутом длины n, если существует последовательность V₁, V₂, ... V_n необязательно различных вершин, таких, что E_i = (V_i-1,V _i ).

Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины.

Вершина, Узел — базовое понятие: точка, где могут сходиться/выходить рёбра и/или дуги. Множество вершин графа G обозначается V(G). Перекрёсток - вершина. Ребро графа — базовое понятие. Ребро соединяет две вершины графа. Дорога – ребро.

Дуга— это ориентированное ребро. Взвешенный граф — граф, каждому ребру которого поставлено в соответствие некое значение (вес ребра). Вес ребра — значение, поставленное в соответствие данному ребру взвешенного графа. Обычно, вес - вещественное число, в таком случае его можно интерпретировать как «длину» ребра. Длина дороги — вес ребра.

Дерево — одна из наиболее широко распространённых структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рёбра графа не должны быть ориентированными. В дополнение к этим трём ограничениям, в некоторых источниках указываются, что рёбра графа не должны быть взвешенными (Рис. 4)

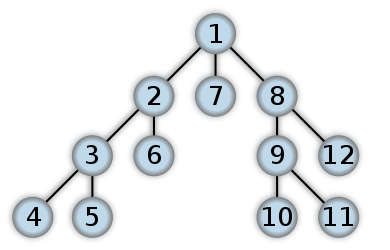
Рис.4