§ 1. Составление двойственной задачи

Рассмотрим две задачи линейного программирования:

Максимизировать функцию

F= +…+

при ограничениях

+…+ ≤

+…+ ≤

………………………

+…+ ≤

Минимизировать функцию

Z= +…+

при ограничениях

+…+ ≤

+…+ ≤

………………………

+…+ ≤

ЭТИ задачи обладают следующими свойствами:

1e. В одной задаче ищется максимум линейной формы, а в другой — минимум.

2е. Коэффициенты при переменных в линейной форме одной задачи являются свободными членами системы ограничений другой задачи, наоборот, свободные члены системы ограничений одной задачи — коэффициентами при переменных в линейной форме другой задачи.

3°. В каждой задаче система ограничений задается в виде неравенств, причем все они одного смысла, а именно: при нахождении максимума линейной формы эти неравенства имеют вид , а при нахождении минимума — вид ≥

4°. Коэффициенты при переменных в системах ограничений описываются матрицами

… …

… …

A= . . . . . . . . . . и A' ^{= . . . . . . . . . . . . . . . ,}

. . . . . . . . . . . . . . . . . . . .

… …

которые являются транспонированными относительно друг друга.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи.

6°. Условия не отрицательности переменных сохраняются в обеих задачах.

Две задачи линейного программирования, удовлетворяющие указанным выше условиям, называются симметричными взаимно двойственными задачами. Мы будем изучать только симметричные двойственные задачи, а поэтому будем называть их короче — двойственными задачами.

Таким образом, каждой задаче линейного программирования можно поставить в соответствие двойственную ей задачу. Первоначальную задачу будем называть исходной (или прямой). Прямая и двойственная венная ей задача, взятые вместе, образуют пару взаимно двойственных задач, причем любую из них можно рассматривать как исходную, тогда другая окажется двойственной ей.

Из сказанного вытекают следующие правила составления задачи, двойственной по отношению к исходной:

1. Приводят все неравенства системы ограничений исходной задачи к неравенствам одного смысла: если в исходной задаче ищется максимум линейной формы — к виду если же минимум — к виду

Для этого неравенства, в которых это требование не выполняется, умножают на — 1.

2. Выписывают матрицу А коэффициентов при переменных исходной задачи, полученных после преобразования п. 1, и составляют матрицу А', транспонированную относительно матрицы А.

3. Составляют систему ограничений двойственной задачи, взяв в качестве коэффициентов при переменных элементы матрицы А', а в качестве свободных членов — коэффициенты при переменных в линейной форме исходной задачи, и записывают неравенства противоположного смысла по сравнению с неравенствами, полученными в п. 1.

4. Составляют линейную форму двойственной задачи, приняв за коэффициенты при переменных свободные члены системы ограничений исходной задачи, полученные в п. I.

5. Указывают, что необходимо найти при решении двойственной задачи, а именно: минимум линейной формы, если в исходной задаче ищется максимум, и максимум, если в исходной задаче ищется минимум.

6. Записывают условие неотрицательности переменных двойственной задачи.

Пример. Составить задачу, двойственную следующей: найти максимум функции F = 3 + при ограничениях

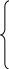- 2 ≤ 2 ,

- + ≤ 2 ,

+ ≤ 1 ,

+ ≤ 5 ,

≥ 0 , ≥ 0.

∆Третье неравенство системы (*) не удовлетворяет п. 1 правил составления двойственной задачи. Поэтому умножим его на —1:

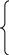- 2 ≤ 2 ,

+ ≤ 2 ,

- ≤ -1 ,

+ ≤ 5.

Д ля облегчения составления двойственной задачи лучше пользоваться расширенной матрицей В, в которую наряду с коэффициентами при переменных системы ограничений исходной задачи запишем свободные члены и коэффициенты при переменных в линейной форме, выделив для этой цели дополнительные столбец и строку. Матрицу В транспонируем и, используя транспонированнуюматрицу В', составляем задачу, двойственную исходной. В данном случае матрицы В и В' имеют вид

1 -2 2

B = -1 1 2 , B= 1 -1 -1 1 3

-1 -1 -1 -2 1 -1 1 1

1 1 5 2 2 -1 5 Z

3 1 F

Двойственная задача сводится к нахождению минимума функции Z = 2 + 2 - + 5 при ограничениях

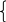- - + ≥ 3 ,

-2 + - + ≥ 1 ,

≥ 0, ≥ 0, ≥ 0, ≥ 0.