§ 4. Некоторые частные случаи
Во всех рассмотренных выше задачах, решенных с помощью симплексного метода, система ограничений оказывалась совместной и имелся конечный оптимум, причем единственный.
Проиллюстрируем на примерах, когда эти условия нарушаются.
Пример I. Найти максимум функции F= +2 при ограничениях
-
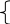2
+3
≤9
-2 ≤2
≥0 ≥0
∆
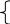Введем добавочные
неотрицательные переменные и сведем
систему ограничений-неравенств к системе
уравнений
-2 +3 + =9
-2 +
0
(j=1,2,3,4)
Получили два уравнения с четырьмя переменными. Если взять за основные переменные и , то исходное базисное решение (0; 0; 9,2) — допустимое.
I шаг . Основные переменные: , ; неосновные переменные: , . Выразим основные переменные и линейную форму через неосновные:
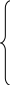=9+
-3
=2- +2
F= +2
Переводим
в основные переменные, так как
входит в выражение F с большим положительным
коэффициентом. Полагаем
=
min {9/3: 
}
= 3. При
= 3 имеем
= 0 и
переходит в неосновные переменные.
IIшаг. Основные переменные: , ; неосновные переменные : , . Выразив основные переменные и линейную форму через неосновные, получим
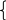=3+(2/3)
-
(1/3)
=8+(1/3) - (2/3)
F=6+(7/3) -(2/3)
Из выражения функции F следует, что переменную нужно перевести в основные. Полагая = min {∞; ∞}, заключаем, что переменная может возрастать неограниченно (ни переменная , ни при этом не станут отрицательными). Значит, и функция F, максимум которой требуется найти, также может неограниченно возрастать. Поэтому можно записать, что Fmax = ∞.q
Ранее (см пример 2 § 6 гл. 14) было дано геометрическое решение этого примера и показано, что данная система неравенств имеет неограниченную область решений и линейная форма при этих ограничениях может принимать сколь угодно большое значение. ▲
Пример 3. Найти максимум функции F = — при ограничениях
-
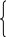2
+3
≤9
- ≤2
+ ≤8
≥0 ≥0.
Введением добавочных неотрицательных переменных сведем систему не¬равенств к системе уравнений
-
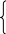2
+3
+
=9
- + =2
+ + =8
Взяв в качестве основных добавочные переменные, получим базисное решение (0; 0; 9; 2, 8), которое является допустимым, поэтому его можно принять за исходное на I шаге решения.
I шаг. Основные переменные: , , ; неосновные переменные ; . Выразим основные переменные и линейную форму через неосновные:
=9+2
-3
=2- +
F= -
=8- -
Переводим в основные переменные. Находим = min {∞; 2/1; 8/1} = 2. При = 2 имеем = 0 и переходит в неосновные переменные.
IIшаг. Основные переменные'. , неосновные переменные: . Имеем
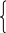=2+
-
=13- -2
=6-2 +
F=2+ - - =2-
В выражении линейной формы F отсутствует одна из неосновных переменных , а критерий оптимальности выполнен (можно считать, что входит в выражение F с нулевым коэффициентом). Поэтому эта переменная не является ни выгодной, ни невыгодной.
Попробуем все же перевести в основные переменные. Полагая = = min( ∞; ∞; 6/2} = 3, заключаем, что переходит в неосновные переменные.
III шаг. Основные переменные: *ь *2, х3; неосновные переменные: xit *5. Имеем
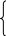=5-0,5
-0,5
=3+0,5 -0,5
=10-2,5 +0,5
F=2-
Таким образом, и на этом шаге получается то же самое выражение линейной формы, а критерий оптимальности снова выполнен.
Па II шаге оптимальное решение имело компоненты (2; 0; 13; 0; 6), а на III шаге — (5; 3; 10; 0; 0). Однако оба оптимальных решения дают одно и то же максимальное значение: Fmax = 2.
Отсюда следует, что единственность оптимального решения может нарушаться. Это происходит в том случае, когда на каком-то шаге решения критерий оптимальности выполняется, а в выражении линейной формы отсутствует одна из неосновных переменных.
При геометрическом решении было установлено, что оптимальными решениями являются все точки отрезка .