СИМПЛЕКСНЫЙ МЕТОД

Симплексный метод является универсальным методом, которым можно решить любую задачу линейного программирования. Идея симплексного метода состоит в следующем. Используя систему ограничений, приведенную к общему виду, т. е. к системе т линейных уравнений с п переменными (т < л), находят ее любое базисное решение, по возможности наиболее простое. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то переходят к другому допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении линейная форма если и не достигнет оптимума, то приблизится к нему . С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.

Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляют переход к другим базисным решениям, которые позволяют приблизиться к области допустимых решений, пока на каком-то шаге не получится допустимое базисное решение. После этого к нему применяют механизм симплексного метода, изложенный выше.

Таким образом, применение симплексного метода распадается на два этапа: I) нахождение допустимого базисного решения системы ограничений; 2) нахождение оптимального решения. При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Так как число базисных решений всегда ограничено, то ограничено и число шагов симплексного метода.

Рассмотрим одну из задач, решаемых симплексным методом.

§ I. Задача об использовании сырья

Эта задача является частным случаем задачи об использовании ресурсов, которая была сформулирована в $ I гл. 14.

Задача. Для изготовления шкафов и буфетов деревообделочный завод применяет древесину четырех видов. Запасы древесины по каждому виду ограничены и составляют соответственно 120, 160, 120, 80 ед. Количество единиц древесины каждого вида, необходимое для изготовления одного шкафа н одного буфета, а также прибыль, получаемая заводом от реализации единицы продукции, даны в табл. 15.1.

Требуется составить такой план выпуска продукции, который бы обеспечил предприятию наибольшую прибыль от реализации всей продукции.

А Дадим математическую формулировку задачи. Пусть и — соответственно количество шкафов и буфетов, запланированных кпроизводству.

Таблица 15.1

виддревис. Запасы древис. Количество древис. необход. для про-ва един.прод-и.

шкафы буфеты

1 120 0 4

2 160 4 0

3 120 2 2

4 80 1 2

Прибыль : 2 3

Так как количество древесины по каждому виду ограничено, то должны выполняться следующие неравенства:

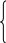
Эта система неравенств и является системой ограничений данной задачи. Целевая функция (линейная форма), выражающая прибыль предприятия, имеет вид

Итак, задача сводится к нахождению максимума функции при ограничениях

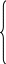
Для сведения системы ограничений-неравенств к системе уравнений прибавим к левой части каждого неравенства добавочные неотрицательные переменные х„ хь, хь. В условиях данной задачи они имеют конкретное экономическое содержание, а именно выражают объем остатков древесины каждого вида после выполнения плана по выпуску продукции. После введения добавочных переменных получим систему уравнений

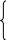
+ 2 + =120

+ 2 + = 80.

Нужно найти такое допустимое базисное решение этой системы ограничений, которое бы максимизировало линейную форму F= 2 + 3

Так как система ограничений есть система четырех независимых уравнений с шестью переменными, то число основных переменных должно равняться четырем, а число неосновных — двум.

Для решения задачи симплексным методом прежде всего нужно найти любое базисное решение. В данном случае это легко сделать. Для этого достаточно взять в качестве основных добавочные переменные . Так как коэффициенты при этих переменных образуют единичную матрицу, то отпадает необходимость вычислять определитель. Считая неосновные переменные и равными нулю, получим базисное решение (0; 0; 120; 160; 120; 80), которое к тому же оказалось допустимым. Поэтому здесь отпадает надобность в применении первого этапа симплексного метода. Переходим сразу ко второму этапу, т. е. к поискам оптимального решения.

I шаг. Основные переменные: неосновные переменные: . В системе (15.1) основные переменные выразим через неосновные. Для того чтобы судить, оставить ли неосновные переменные в числе неосновных или их выгоднее с точки зрения приближения к оптимальному решению перевести в основные, следует выразить через них и линейную форму (в данном случае она уже выражена через переменные и ). Тогда получим

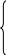
= 120 – 4

= 160 – 4

= 120 - 2 - 2

= 80 - - 2

F = 2 +3

При = имеем = 120, =160, =120, = 80, что дает базисное решение (0; 0; 120; 160; 120; 80), которое мы приняли за исходное. При этом базисном решении значение линейной формы F = 2 + З = 0.

Когда мы полагали = = 0 (завод ничего не выпускает), была поставлена цель — найти первое, безразлично какое, базисное решение. Эта цель достигнута. Теперь от этого первоначального решения нужно перейти к другому, при котором значение линейной формы увеличится. Из рассмотрения линейной формы видно, что ее значение возрастает при увеличении значений переменных и . Иными словами, эти переменные невыгодно считать неосновными, т. е. равными нулю, их нужно перевести вчисло основных. Это и означает переход к новому базисному решению. При симплексном метоле на каждом шаге решения предполагается перевод в число основных только одной из свободных переменных. Переведем в число основных переменную xt, так как она входит в выражение линейной формы с большим коэффициентом.

Как только одна из свободных переменных переходит о число основных, одна из основных должна быть переведена на ее место в число неосновных. Какую же из четырех основных переменных нужно вывести? Ответить на этот вопрос помогут следующие рассуждения.

Значение необходимо сделать как можно большим, так как это соответствует конечной цели — максимизации F. Однако оказывается, что увеличение х% может продолжаться только до известных границ, а именно до тех пор, пока не нарушится требование не отрицательности переменных. Так, из первого уравнения системы (15.2) следует, что переменная не должна превышать числа 120/4, т. е. 90, поскольку только при этих значениях переменная остается положительной (если — 30, то = 0; если же >30, то < 0). Из третьего уравнения системы (15.2) следует, что < 120/2, т. е. х% < 60, из четвертого — что < 80/2, т. е. < 40 (во второе уpавнение переменная не входит). Всем этим условиям удовлетворяет < 30.

Иными словами, для ответа на вопрос, какую переменную нужно перевести в число неосновных, нужно принять {120/4; 120/2; 80/2) — min {30; 60; 40) = min {30 60 40} =30 Тогда = 0 и переходит в число неосновных переменных, а и останутся положительными.

II шаг. Основные переменные: , , неосновные переменные: Выразим основные переменные и линейную форму через неосновные. В системе (15.2) берем то уравнение, из которого получено минимальное значение отношения свободного члена к коэффициенту при . В данном случае это первое уравнение, которое выделено рамкой. Выразив из этого уравнения имеем = 30 — 0,25 . Подставим это выражение во все остальные уравнения системы (15.2) и в линейную форму F и, приведя подобные члены, получим

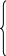= 30 – 0,25

= 160 – 4

= 60 - 2 +0,5

= 20 - + 0,5

F= 90 + 2 - 0,75

При = = 0 имеем F = 90. Это уже лучше, чем на I шаге, во не искомый максимум. Дальнейшее увеличение функции F возможно за счет введения переменной в число основных; так как эта переменная входит в выражение F с положительным коэффициентом, поэтому ее увеличение приводит к увеличению линейной формы и ее невыгодно считать неосновной, т. е. равной нулю.

Для ответа на вопрос, какую переменную вывести из основных в неосновные, примем = min {160/4; 60/2; 20/1) = 20. Тогда - переходит в число неосновных переменных, а и остаются при этом положительными.

Первое уравнение не используется при нахождении указанного минимума, так как не входит в это уравнение.

Ill шаг. Основные переменные: неосновные переменные: Выразим основные переменные и линейную форму через неосновные. Из последнего уравнения системы (15.3) (оно выделено) имеем 20 + 0,5 — . Подставляя это выражение в остальные уравнения и в линейную форму, получим.

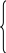= 20 + 0,5

30 —0,25

80 - 2 + 4

20—0,5 + 2

F = 130 + 0,25 —2

Из выражения линейной формы следует, что ее максимальное значение еще не получено, так как возможно увеличение F за счет введения в основные переменной , (она имеет положительный коэффициент). Полагаем = min {∞; 30/0,25; 80/2; 20/0,5) =40.

Здесь мы впервые встречаемся с двумя положениями, которые требуют дополнительных разъяснений.

Во-первых, хотя переменная и входит в выражение для , {первое уравнение системы (15.4)}, но имеет положительный коэффициент и при любом возрастании переменная не может стать отрицательной. Иными словами, в первом уравнении никаких ограничений на возрастание переменной х9 не накладывается, поэтому мы условно пишем ∞. Условимся в дальнейшем пользоваться этим же обозначением, если переменная, вновь вводимая в число основных, не входит в какое-либо уравнение системы ограничений.

Во-вторых, мы получим два одинаковых минимальных значения, равные 40. Если = 40, то = 0 и = 0, т. е. напрашивается вывод, что вместо одной переменной нужно перевести в число неосновных сразу две: и . Но число основных переменных не должно быть меньше четырех. Как же быть в этом случае? Для этого поступают следующим образом. Одну из переменных ( или ) оставляют в числе основных, но при этом ее значение считают равным нулю, т. е. полученное на следующем шаге базисное решение оказывается вырожденным. Оставим, например, в числе основных переменных, а переведем в число неосновных.

IV шаг. Основные переменные: ; неосновные переменные: , . Выразим основные переменные и линейную форму F через неосновные, начав это выражение из четвертого уравнения системы (15.4). В итоге получим

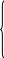
40— —

20 + 0,5

40 — 2 + 4

0 + 4 - 4

F = 140—0,5 —

Так как в выражение линейной формы переменные и входят с отрицательным коэффициентами, то никакое увеличение F за счет этих переменных невозможно.

Отсутствие на каком-то шаге симплексного метода в выражении линейной формы F, максимум которой ищется, неосновных переменных с положительными коэффициентами является критерием оптимальности.

Следовательно, на IV шаге критерий оптимальности достигнут и задача решена. Оптимальным служит решение (40; 20; 40; 0; 0; 0), при котором = 140. Таким образом, для получения наибольшей прибыли, равной 140 ден. ед., из данных запасов древесины завод должен изготовить 40 шкафов и 20 буфетов. При этом древесина II, III и IV видов окажется использованной полностью, а 40 ед. древесины 1 вида останутся неизрасходованными. ▲