2. Логика предикатов

2.1. Предикаты

В исчислении предикатов во внимание принимают не только истинностное значение элементарного высказывания, но и его предмет – тот объект, о котором идет речь в высказывании. Иначе говоря, высказывание в исчислении предикатов рассматривается не как нечто неделимое, но как состоящее из двух частей – собственно высказывания и предмета высказывания. Первая часть в нем – это что именно высказывается, а вторая – про что или про кого это высказывание. В переводе с английского predicate означает сказуемое, т.е. как раз то, что высказывается, поэтому первая часть в высказывании так и называется – предикат. Например, в высказывании «число 6 является простым» «число 6» будет предметом, а «является простым» – предикатом. В языке ИП предусматриваются средства для обозначения предикатов – предикатные переменные и предметов – предметные переменные.

Истинностное значение высказывания, расчлененного на предикат и предмет, зависит как от того, так и другого.

Классификация предикатов:

Равносильность и следование предикатов.

Теорема1.

Теорема2.

Теорема3.

2.2. Логические и кванторные операции над предикатами

Поскольку значениями предикатов являются высказывания, к предикатам можно применять все логические операции, определенные для высказываний.

Отрицание.

Теорема.

Конъюнкция.

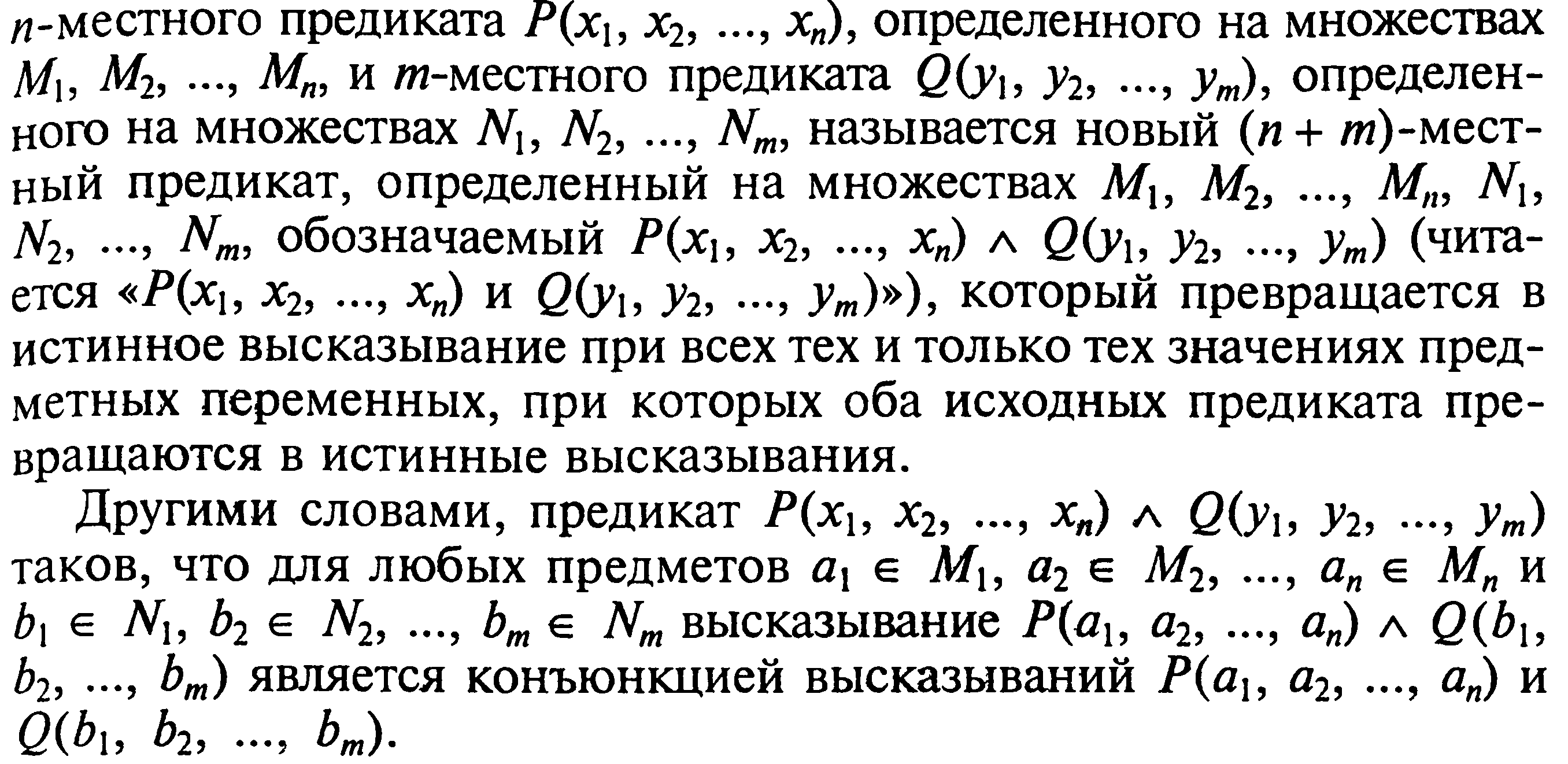
Теорема.

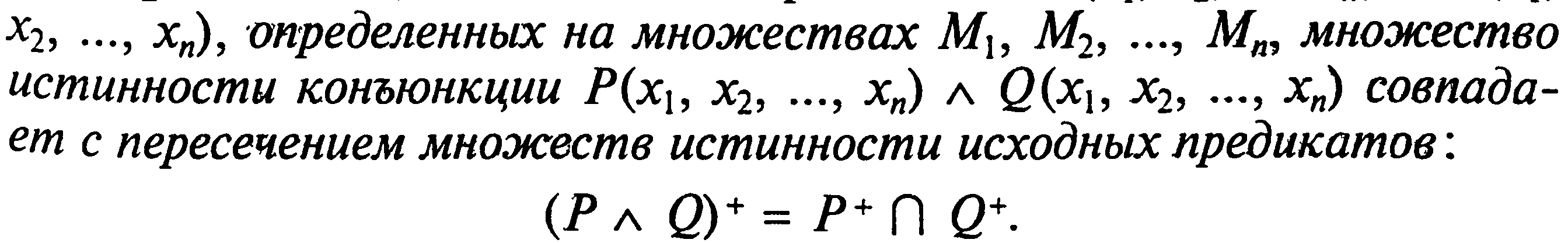
Дизъюнкция.

Теорема.

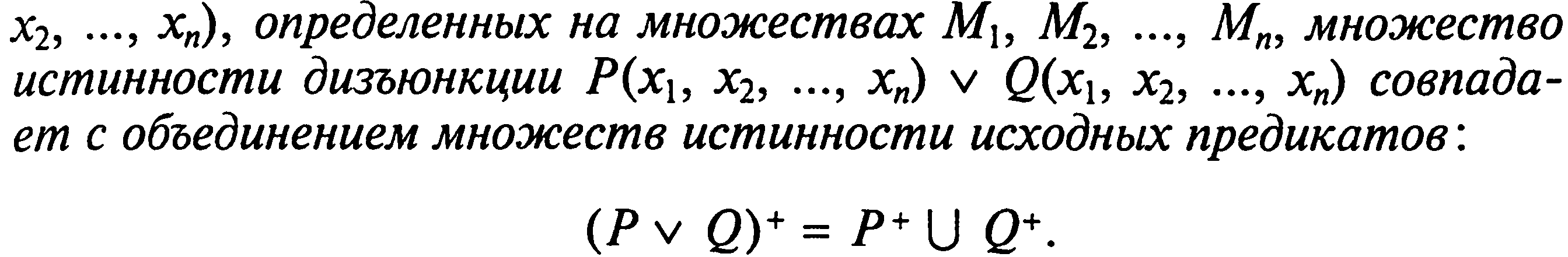
Импликация и эквивалентность.

Кроме того, над предикатами определяются две новые операции, называемые кванторными (кванторами).

Как и операция ¬, каждый квантор является унарной операцией, т.е. действует на одиночный предикат, но, в отличие от ¬, связывает некоторый из аргументов последнего, давая в качестве результата предикат, не зависящий от этого аргумента и определяемый следующим образом.

Квантор (все)общности.

.

К n-местному предикату можно применить n кванторов. Применение квантора к n-местному предикату (n≥1) дает (n-1)-местный предикат.

Квантор существования.

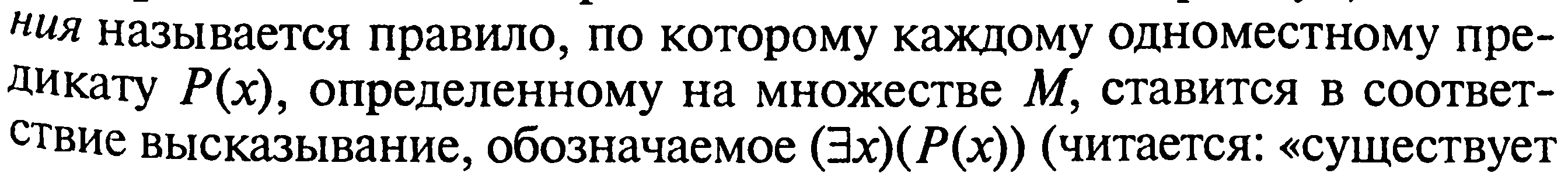
2.3. Формулы логики предикатов и их классификация

Формулы логики предикатов строятся из предметных и предикатных переменных, символов логических операций ¬, , , →, ↔, , и знаков пунктуации ( , ). Назначение предметных переменных - обозначать возможные предметы, назначение предикатных переменных- обозначать возможные предикаты. Иначе говоря, предметная и предикатная переменные - это некоторые буквы, вместо которых можно иногда подставлять в качестве значений конкретные предметы и конкретные предикаты соответственно. В дальнейшем в их роли будут употребляться соответственно малые и большие буквы конца латинского алфавита, возможно, с индексами. Предикатные переменные со значениями n-местных предикатов называются n-местными предикатными переменными. При n = 0 они являются высказывательными переменными.

Индуктивное определение формулы логики предикатов:

Подформулой элементарной формулы является сама формула; подформулами составных формул, кроме них самих, считаются все подформулы их составляющих F₁ и F₂.

Относительно правил опускания и расстановки скобок в формулах: кванторы связывают сильнее других операций.

Любая формула логики предикатов только тогда имеет смысл (что-то выражает), когда имеется какая-нибудь интерпретация входящих в нее символов.