Ответы на экзаменационные вопросы. Введение

Логика – это наука о законах правильного мышления.

Ее основные задачи:

1) анализ правильности рассуждений (состоит в выяснении, является ли данное рассуждение доказательным),

2) синтез правильных рассуждений (состоит в построении таких рассуждений, которые имеют доказательную силу, являются доказательствами).

В математической логике обе эти задачи решаются математическими методами. Отличительной особенностью любого математического метода является отвлечение (абстрагирование) от содержания рассуждений. Иначе говоря, в математических методах внимание обращается исключительно на форму и совершенно игнорируется содержание рассуждения.

1. Логика высказываний

1.1. Высказывания и логические операции над ними

Под высказыванием мы понимаем всякое повествовательное предложение, о котором имеет смысл говорить, что оно истинно или ложно.

Пример.

Предложение «Страусы летают» выражает ложное высказывание, а предложение «Курение вредит Вашему здоровью» – истинное высказывание.

Предполагается, что каждое высказывание является либо истинным, либо ложным, но не тем и другим одновременно и никаким иным. Именно это свойство высказываний – быть истинным или ложным – и будет нас интересовать, от структуры и содержания высказывания мы отвлекаемся.

Обозначив истинное высказывание символом 1 (или и), а ложное – 0 (или л), вводится функция , заданная на совокупности всех высказываний и принимающая значения в множестве {1,0}, по правилу:

Над высказываниями определяются следующие основные логические операции (логические связки), с помощью которых можно из простых высказываний строить новые (составные высказывания):

.

Отрицание высказывания P есть высказывание, истинное тогда и только тогда, когда ложно высказывание P.

Конъюнкция высказываний P, Q представляет собой высказывание, истинное тогда и только тогда, когда истинны оба высказывания P, Q. Последние называются конъюнктивными членами конъюнкции .

.

Дизъюнкция высказываний P, Q является высказыванием, истинным тогда и только тогда, когда истинно по меньшей мере одно из высказываний P, Q. Высказывания P и Q называются дизъюнктивными членами дизъюнкции PQ.

Импликация высказываний P, Q есть высказывание, ложное тогда и только тогда, когда истинно высказывание P и ложно высказывание Q. Высказывания P и Q называются соответственно посылкой и заключением импликации P→Q.

Эквивалентность высказываний P, Q представляет собой высказывание, истинное тогда и только тогда, когда одновременно истинны или одновременно ложны высказывания P, Q.

Каждую из этих операций можно рассматривать как операцию над символами (логическими константами) 0 и 1 (или и и л).

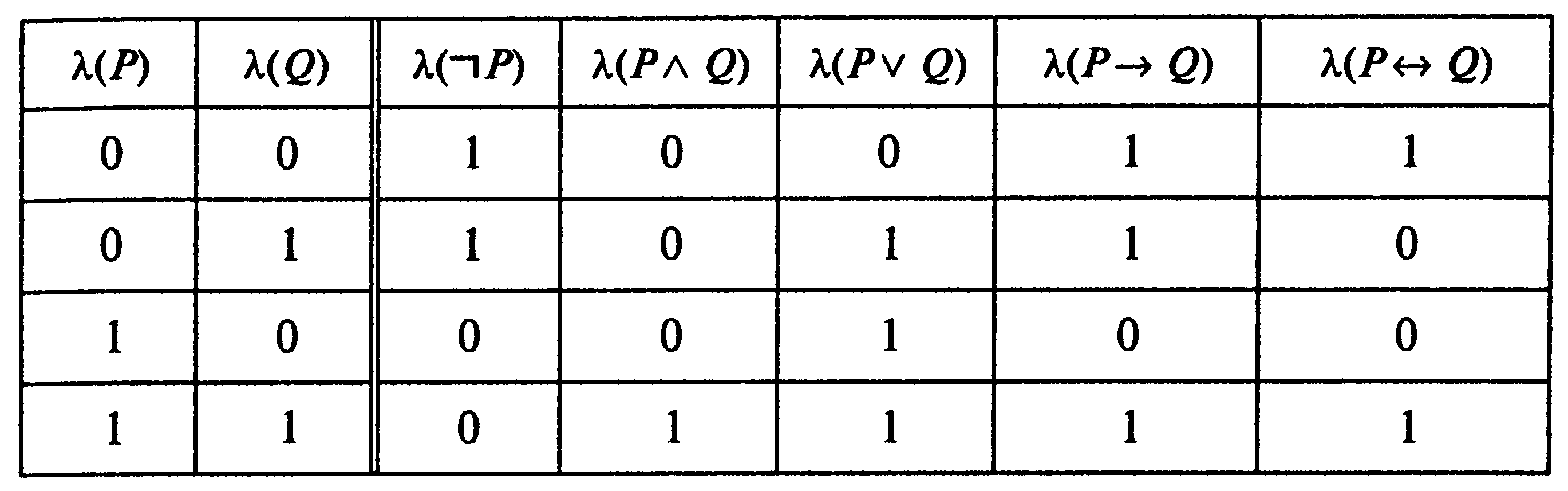
1.2. Формулы логики высказываний и их классификация

Пропозициональными (высказывательными) переменными называются такие переменные, вместо которых можно подставлять конкретные высказывания.

Обозначаются они чаще всего большими буквами конца латинского алфавита, возможно, с индексами: P, Q, ..., Y, Z, P₁, Q₂, X_i и т.п.

Из пропозициональных переменных при помощи логических операций (связок) можно строить формулы. Формула в логике высказываний определяется индуктивно следующим образом:

Скобки в формулах, как обычно, указывают порядок действий. Разрешается опускать внешние скобки.

Для обозначения формул будут применяться большие буквы начала латинского алфавита, возможно, с индексами: A, B, C_i, и т.п. Запись F(X₁, ..., X_n) означает, что F есть формула в переменных X₁, ..., X_n, т.е. что всякая пропозициональная переменная, входящая в F, принадлежит списку переменных X₁, ..., X_n.

Части формулы, которые сами являются формулами, называются подформулами данной формулы.

Любая формула логики высказываний сама по себе ничего не выражает, но она становится высказыванием всякий раз, когда под каждой переменной в ней подразумевается некоторое конкретное высказывание, т.е. когда для каждой такой переменной задано конкретное истинностное значение (интерпретация). Истинностное значение этого высказывания однозначно определяется формулой и интерпретацией ее переменных: