33. Рух частинки через потенціальний бар’єр. Тунельний ефект.

Розглянемо одноманітний фінітний рух частинки, яка рухається в потенціальному полі U=U(x,y,z), який має максимум, який поділяє увесь простір на дві області. В кожній з якій енергія частинки є меншою ніж E<U_max . Такий вигляд потенційної енергії носить назву потенційного бар’єру. Згідно з класичною механікою, рух частинки у потенційному полі U(x) характеризується тим, що при E<U(х) частинка не може пройти область максимуму, а значить вона зупиниться в деякій точці х₁ і почне рухатися в протилежному напрямку(відіб’ється), т. х₁ називається класичною точкою повороту. Такий бар’єр E<U(х) називається високим і для нього коефіцієнт підбивання Е рівне 1. R=1, D=0. Якщо ж E>U(х) , то вона пройде через бар’єр, а отже коефіцієнт R=0, D=1. Такі результати одержали в результаті класичного підходу до розглядуваної проблеми.

Квантова механіка дає результати відмінні від граничних класичних, тобто R 0;1, D 0;1. Має місце проникнення частинки під бар’єр, тобто ймовірність буде мати певних значень і знаходження даної ймовірності складає предмет квантової механіки задачі проходження частинки через бар’єр.

Розглянемо спочатку просту форму бар’єра – прямокутний потенціальний бар’єр нескінченної ширини. Розрахуємо коефіцієнт відбивання . Оскільки ,

Задача зводиться до розрахункових коефіцієнтів A₁,B₁ які визначають ймовірність руху частинки в напрямі осі Х і в зворотньому.

Для визначенння цих коефіцієнтів необзхідно розвязати рівняння Шредінгера і для цього увесьпростір розібємо на дві області, для кожної з них запишем рівняння Шредінгера

I: (15.1)

II:

Перепишем 15.1 (15.2)

Введемо позначення (15.3)

(15.4)

З урахуванням 15,3 і 15,4 систему 15,2 (15.5)

(15.6)

Розв’язком рівнянь буде (15.7)

(15.8)

Оскільки в області II області зворотнього руху частинок відсутній, то B₂₌₀

Для знаходження коефіцієнта скористаємося умовами неперервності хвильової функції та їх похідних(умовами зшивання) і

Застосовуючи до рівнянь (15,7) і (15,8) (15.10)

Розв’язуючи систему рівнянь відносно A₁ і B₁ одержимо

З урахуванням (15,3) і (15,4) (15.11)

Отримаємо значення коефіцієнтів відбивання R<1 ,D<1, що відрізняються від класичного розв’язку

Для випадку високого прямокутного бар’єра(E<U₀) нескінченної ширини, отримаємо результати аналогічні розв’язкам(15,11)

Низькі потенціальні бар’єри характеризуються показником заломлення (15.12)

- Довжина хвилі Деброля мікрочастинок, що падають на бар’єр, -Довжина хвилі Деброля відбитих від бар’єру мікрочастинок.

Розглянемо більш загальний випадок, а саме прямокутний потенціальний бар’єр скінченної ширини, причому бар’єр є високим

Знайдемо коефіцієнт відбивання і пропускання для даного випадку. Для цього розіб’ємо весь простір на 3 області і для кожної з них запишемо рівняння Шредінгера

; ; (15.13)

Спростимо ; ;

(15.14)

Введемо позначення (15.15)

(15.16)

(15.17)

З урахуванням (15.15)-(15,17) (15,14) (15.18)

Запишемо розв’язки для кожного з (15,18)

(15.19)

Щоб окремі розв’язки (15,19) утворювали єдину хвильову функцію у полі бар’єра потрібно задовольнити умові неперервного переходу розв’язків і їх перших похідних по краях бар’єру

Тобто, і (15.20)

Розв’язуючи систему рівнянь , отримаємо наступний вираз для коефіцієнтів пропускання

, (15.22)

Розглянемо випадки

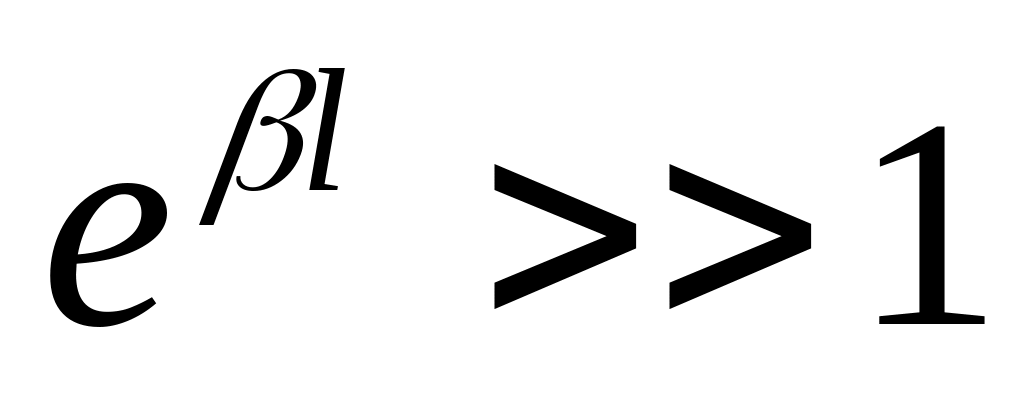1. , Тоді вираз (15,22) спрощується (15.23)

2. E=U

Вираз (15,23) може бути записаний (15.24)

D₀ - Нормальний множник, як правило = 1.

Для випадку E>U₀ квантова механіка розв’язок не дає повної прозорості бар’єра як цього вимагає класична механіка, якщо ж E<U₀ коефіцієнт проходження відмінний від 0, тобто має місце проникнення частинки під бар’єр і це явище отримало назву тунельного ефекту. Він має суто квантово -механічний зміст і не можливий у класичній фізиці.

Тунельний ефект лежить в основі багатьох важливих процесів атомної молекулярної фізики, атомного ядра і твердого тіла

Прикладом прояву тунельного ефекту є емісія електронів з металу α розпад радіоактивних ядер без тунельного ефекту не можливе протікання ядерних реакцій. Ми розглянули прямокутний бар’єр в реальному ж маємо справу з бар’єром довільної форми, тоді співвідношення (15,24) (15.25)