14.2. Числовые характеристики непрерывной случайной величины

Определение 4. Математическое ожидание непрерывной случайной величины определяется по формуле , при условии, что интеграл абсолютно сходится.

Замечание 1. Определение корректно, так как . Для интегральной функции распределения можно построить интегральную сумму, в которой перейти к пределу при .

Замечание 2. В силу замечания 1 для непрерывных случайных величин остаются справедливыми свойства математического ожидания и дисперсии.

Определение 5. Дисперсия непрерывной случайной величины определяется по формуле при условии, что интеграл абсолютно сходится.

Замечание. Дисперсия непрерывной случайной величины также является постоянной величиной.

Определение 6. Средним квадратичным отклонением (СКО) случайной величины Х называется величина .

Определение 7. Модой непрерывной случайной величины Х называется то её значение, при котором плотность распределения максимальна.

Замечание. Геометрически мода является абсциссой той точки кривой распределения, ордината которой максимальна. Т.е. чтобы найти моду, нужно найти максимум плотности распределения.

Определение 8. Медианой непрерывной случайной величины Х называется такое её значение , для которого одинаково вероятно, окажется ли случайная величина больше или меньше , то есть .

Замечание. Прямая, проведенная в точке с абсциссой , делит пополам площадь, ограниченную кривой распределения.

Пример 1. Дана плотность вероятности случайной величины :

Найти интегральную функцию распределения этой случайной величины и её числовые характеристики. Построить графики плотности вероятности и интегральной функции распределения.

Решение. 1) Найдём интегральную функцию распределения.

При .

При .

При .

Таким образом,

2) Найдём числовые характеристики случайной величины:

а) математическое ожидание:

;

б) дисперсия:

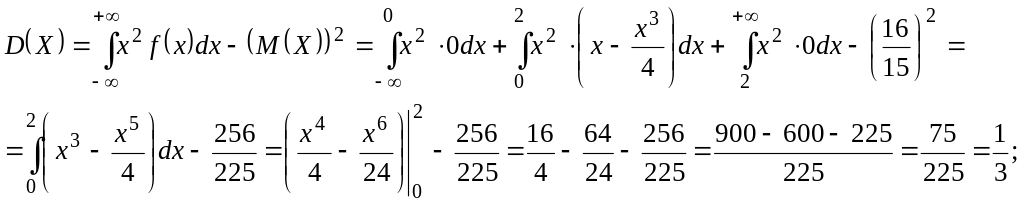
в) СКО: .

г) Мода. Найдём максимум функции . Для этого вычислим первую и вторую производную функции : при , ; , , поэтому в точке плотность распределения достигает максимального значения. Следовательно, мода .

д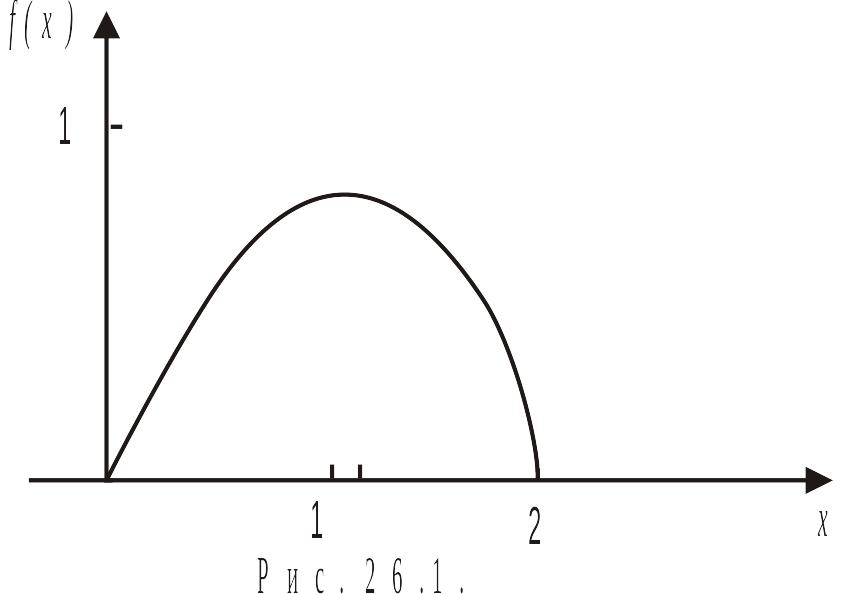 ) Медиана. Найдём медиану из условия . В данном случае . Отсюда для определения медианы получаем уравнение или , откуда . Из четырех корней этого уравнения нужно выбрать тот, который заключен между 0 и 2. Таким образом .

3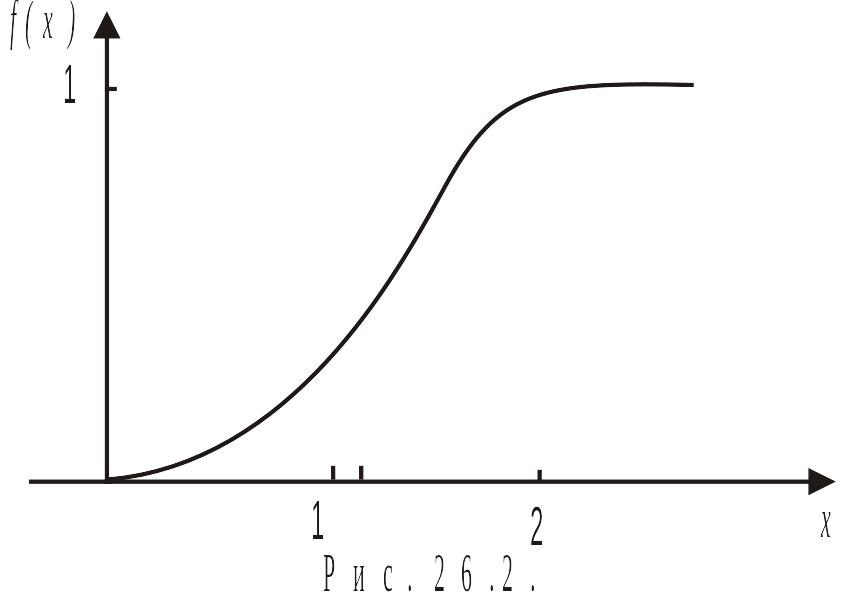 ) Построим график плотности вероятности (рис. 26.1).

Построим график функции распределения (рис. 26.2).

14.3. Некоторые законы распределения непрерывных случайных величин

14.3.1. Равномерное распределение

Определение 9. Равномерный закон распределения непрерывной случайной величины задается функцией плотности распределения вида:

Пример 2. Найти числовые характеристики.

14.3.2. Показательное распределение

Определение 10. Показательный закон распределения непрерывной случайной величины задается функцией плотности распределения вида: где постоянный параметр.

Пример 3. Найти числовые характеристики, интегральную функцию распределения, вероятность попадания в заданный интервал.

Замечание. При проверке гипотезы на наличие у СВ показательного распределения находят выборочное среднее и выборочное СКО, если они близки, то выдвигают гипотезу и проверяют её.