
- •Глава 3. Случайные величины и функции распределения
- •§ 12. Основные свойства функций распределения
- •12.1. Понятие о случайной величине
- •12.2. Свойства функции распределения вероятностей
- •§ 13. Дискретные случайные величины их числовые характеристики и законы распределения
- •13.1. Числовые характеристики дискретных случайных величин
- •13.1.1. Полигон и функция распределения
- •13.1.2. Математическое ожидание
- •13.1.3. Дисперсия и среднее квадратичное отклонение
- •13.1.4. Среднее квадратичное отклонение
- •13.1.5. Другие числовые характеристики
- •13.2. Законы распределения дискретных случайных величин
- •13.2.1. Биномиальное распределение
- •13.2.2. Распределение Пуассона
- •§ 14. Непрерывные случайные величины их числовые характеристики и законы распределения
- •14.1. Функция распределения и плотность распределения непрерывной случайной величины
- •14.2. Числовые характеристики непрерывной случайной величины
- •14.3. Некоторые законы распределения непрерывных случайных величин
- •14.3.1. Равномерное распределение
- •14.3.2. Показательное распределение
- •14.3.3. Нормальное распределение.
- •14.4. Другие числовые характеристики
- •§ 15. Одинаково распределённые взаимно независимые случайные величины
- •§ 16. Закон больших чисел и предельные теоремы теории вероятностей
- •16.1. Неравенства Маркова и Чебышева
- •16.2. Теорема Чебышева
- •16.3. Теорема Бернулли
- •16.4. Теорема Пуассона
- •16.5. Понятие о центральной предельной теореме Ляпунова
- •§ 17. Функции одного случайного аргумента
- •17.1. Распределение функции одного случайного аргумента
- •17.2. Математическое ожидание функции одного случайного аргумента
- •17.3. Функция надёжности
- •17.4. Логарифмически-нормальное распределение
- •§ 18. Функции двух случайных аргументов
- •18.1. Закон распределения суммы независимых случайных величин
- •18.2. Законы распределения, являющиеся функциями нормально распределённых независимых случайных величин
- •18.2.1. Распределение
- •18.2.2. Распределение Стьюдента (псевдоним статистика в. Госсета)
- •18.2.2. Распределение Фишера-Снедекора
- •Глава 4. Многомерные случайные величины
- •§ 19. Понятие о многомерной случайной величине
- •§ 20. Закон распределения вероятностей дискретной двумерной случайной величины
- •§ 21. Функция распределения вероятностей многомерной случайной величины
- •21.1. Определения и геометрический смысл
- •21.2. Свойства функции распределения двумерной случайной величины
- •§ 22. Плотность распределения вероятностей непрерывной двумерной случайной величины
- •22.1. Определение плотности распределения вероятностей
- •22.2. Свойства плотности распределения вероятностей
- •22.3. Дифференциальные функции составляющих двумерной случайной величины
- •22.4. Условные законы распределения составляющих системы непрерывных случайных величин
- •§ 23. Числовые характеристики двумерных случайных величин
- •Свойства условного математического ожидания
- •§ 24. Зависимые и независимые случайные величины
- •24.1. Свойства функций распределения независимых случайных величин
- •24.2. Корреляционный момент системы случайных величин
- •24.3. Коэффициент корреляции системы случайных величин
- •Свойства коэффициента корреляции
- •24.4. Коррелированность и зависимость случайных величин
- •24.5. Свойства математического ожидания и дисперсии для коррелированных случайных величин
- •§ 25. Двумерный нормальный закон распределения
13.1.5. Другие числовые характеристики
Определение 14. Модой дискретной случайной величины Х называется её наиболее вероятное значение.
Замечание. Геометрически мода является абсциссой той точки полигона распределения, ордината которой максимальна.
Определение 15.
Начальным
моментом порядка
![]() случайной
величины Х называется математическое
ожидание величины
случайной
величины Х называется математическое
ожидание величины
![]() :
:
![]() .
.
Замечание 1.
В частности,
![]() ,
,
![]() .
.
Замечание 2.
Пользуясь определением моментов,
дисперсию можно записать в виде
![]() .
.
Замечание 3. Начальные моменты позволяют учесть большие, но маловероятные значения случайной величины.
Определение 16.
Центральным
моментом порядка
случайной
величины Х называется математическое
ожидание величины
![]() :
:
![]() .
.
Замечание 1. В
частности
![]()
![]() .
.
Замечание 2.
Нетрудно показать, что 1)
![]() ,
2)
,
2)
![]() ,
,
3)
![]() .
Моменты более высоких порядков применяются
редко.
.
Моменты более высоких порядков применяются
редко.
Замечание 3. Рассмотренные моменты называют теоретическими.
Пример 1. Случайная величина Х имеет ряд распределения:
|
2 |
4 |
8 |
10 |
|
0,4 |
0,2 |
0,1 |
0,3 |
П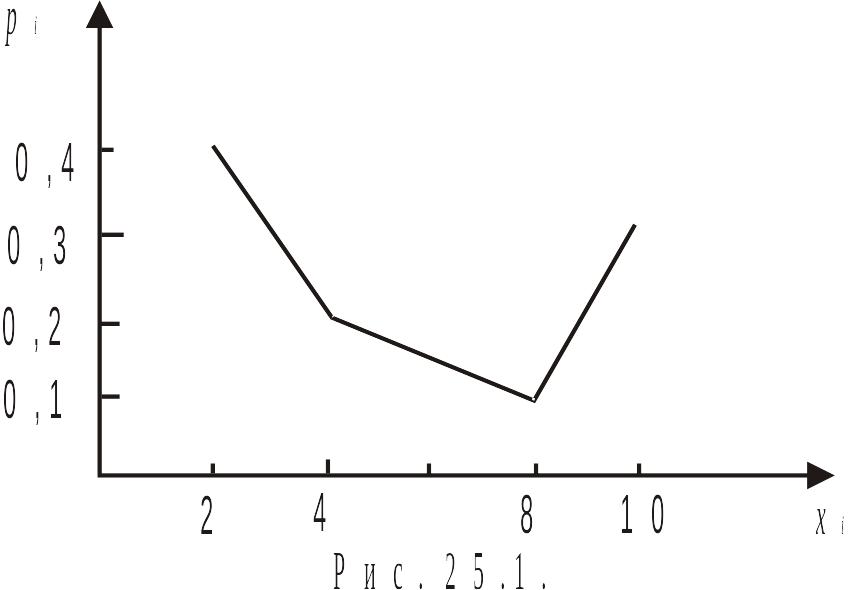 остроить
многоугольник распределения, найти
функцию распределения вероятности и
построить ее, найти математическое
ожидание, дисперсию, СКО и моду случайной
величины Х.
остроить
многоугольник распределения, найти
функцию распределения вероятности и
построить ее, найти математическое
ожидание, дисперсию, СКО и моду случайной
величины Х.
Решение. 1) В прямоугольной системе координат отметим точки и соединим их последовательно ломаными отрезками. Получим многоугольник распределения (см. рис. 25.1).
2) Найдём функцию распределения вероятности.
Если
![]() ,
то
,
то
![]() .
.
Е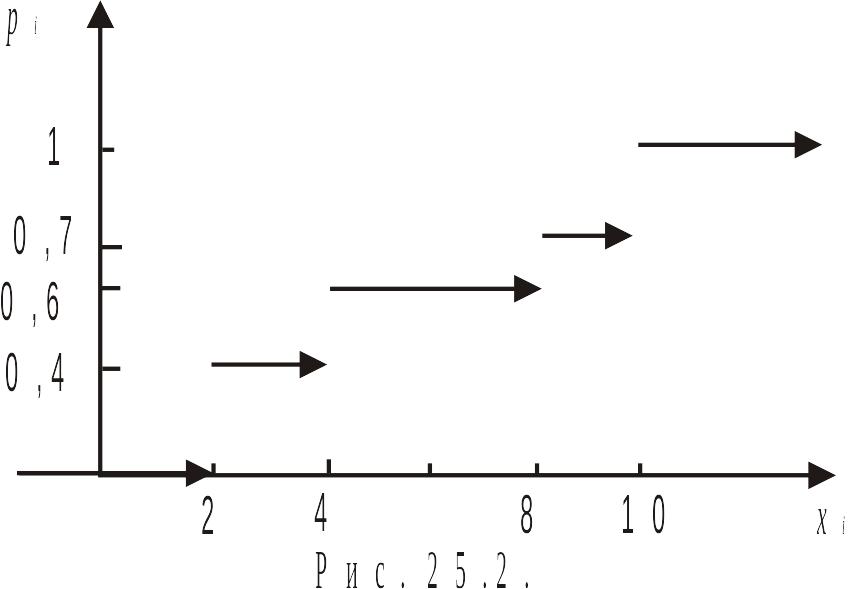 сли
сли
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Построим график функции распределения вероятности (см. рис. 25.2).
3) Найдём числовые характеристики случайной величины Х.
а) математическое
ожидание:
![]() ;
;
б) дисперсия:
![]() ;
;
в) СКО:
![]() ;
;
г) мода случайной
величины Х
– это такое её значение, которому
соответствует наибольшая вероятность;
наибольшая вероятность
![]() соответствует значению
соответствует значению
![]() ;
поэтому
;
поэтому
![]() .
.
13.2. Законы распределения дискретных случайных величин
13.2.1. Биномиальное распределение
Определение 9.
Если
вероятность наступления случайного
события в каждом испытании равна
![]() ,
то вероятность того, что случайное
событие появится в этих
,
то вероятность того, что случайное
событие появится в этих
![]() испытаниях ровно
испытаниях ровно
![]() раз, выражается формулой Бернулли:
раз, выражается формулой Бернулли:
![]() .
Закон распределения дискретной случайной
величины
,
которая может принимать
.
Закон распределения дискретной случайной
величины
,
которая может принимать
![]() значение {0, 1, 2, …,
},
описываемый формулой Бернулли, называется
биномиальным.
значение {0, 1, 2, …,
},
описываемый формулой Бернулли, называется
биномиальным.
Замечание. Для
биномиального закона распределения
![]() ,
,
![]() ,
,
![]() ,
мода
,
мода
![]() .
.
Доказательство.
1) Пусть
случайная величина Х – число наступлений
события А в
независимых испытаниях. Общее число Х
появления события А в этих испытаниях
складывается из чисел появления события
А в отдельных испытаниях. Поэтому, если
случайные величины:
![]() – число появлений события в первом
испытании,
– число появлений события в первом
испытании,
![]() – во втором, и т.д.,
– во втором, и т.д.,
![]() – в
-ом,
то общее число появлений события
– в
-ом,
то общее число появлений события
![]() .
Тогда по свойству 3 математического
ожидания имеем
.
Тогда по свойству 3 математического
ожидания имеем
![]() .
.
2) Так как величины , , … , взаимно независимы (исход каждого испытания не зависит от исходов остальных испытаний), то по свойствам дисперсии
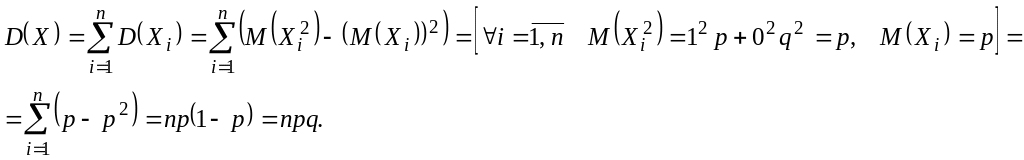
Отсюда следует,
что
![]() Мода (см. § 10):
.
Мода (см. § 10):
.
